Advertisements
Advertisements
प्रश्न
Discuss rolling on an inclined plane and arrive at the expression for acceleration.
उत्तर
Let us assume a round object of mass m and radius R is rolling down an inclined plane without slipping as shown in the figure. There are two forces acting on the object along the inclined plane. One is the component of gravitational force (mg sin θ) and the other is the static frictional force (f). The other component of gravitation force (mg cos θ) is cancelled by the normal force (N) exerted by the plane. As the motion is happening along the incline, we shall write the equation for motion from the free body diagram (FBP) of the object.

Rolling on an inclined plane
For transnational motion, mg sin θ is the supporting force and f is the opposing force, mg sin θ f = ma
For rotational motion, let us take the torque with respect to the center of the object. Then mg sin 0 cannot cause torque as it passes through it but the frictional force f can set torque of Rf = Iα
By using the relation, a = rα, and moment of inertia I = mK2
we get,
Rf = mK2 `a/R`; f = ma `(K^2/R^2)`
Now equation becomes,
mg sin θ – ma `((K^2)/(R^2))` = ma
mg sin θ = ma + ma `(K^2/R^2)`
a `(1+K^2/R^2)` = g sin θ
After rewriting it for acceleration, we get,
a = `(gsinθ)/((1+K^2/R^2))`
We can also find the expression for the final velocity of the rolling object by using the third equation of motion for the inclined plane.
v2 = u2 + 2as. If the body starts rolling from rest, u = 0. When h is the vertical height of the incline, the length of the incline s is, s = `h/sinθ`
`v^2 = 2(g sintheta)/((1 + K^2/R^2))(h/sin theta) = (2gh)/((1 + K^2/R^2))`
By taking square root,
v = `sqrt((2gh)/((1 + K^2/R^2)))`
The time taken for rolling down the incline could also be written from the first equation of motion as, v = u + at. For the object which starts rolling from rest, u = 0. Then,
t = `v/a`
t = `(sqrt((2gh)/((1 + K^2/R^2)))) (((1 + K^2/R^2))/(g sin theta))`
t = `sqrt((2h(1 + K^2/R^2))/(g sin^2theta))`
The equation suggests that for a given incline, the object with the least value of the radius of gyration K will reach the bottom of the incline first.
APPEARS IN
संबंधित प्रश्न
A solid sphere of mass 1 kg rolls on a table with linear speed 2 m/s, find its total kinetic energy.
Can an object be in pure translation as well as in pure rotation?
A hollow sphere and a solid sphere having same mss and same radii are rolled down a rough inclined plane.
A sphere cannot roll on
In rear-wheel drive cars, the engine rotates the rear wheels and the front wheels rotate only because the car moves. If such a car accelerates on a horizontal road the friction
(a) on the rear wheels is in the forward direction
(b) on the front wheels is in the backward direction
(c) on the rear wheels has larger magnitude than the friction on the front wheels
(d) on the car is in the backward direction.
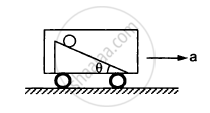
The following figure shows a smooth inclined plane fixed in a car accelerating on a horizontal road. The angle of incline θ is related to the acceleration a of the car as a = g tanθ. If the sphere is set in pure rolling on the incline, _____________.
A string is wrapped over the edge of a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
A hollow sphere is released from the top of an inclined plane of inclination θ. (a) What should be the minimum coefficient of friction between the sphere and the plane to prevent sliding? (b) Find the kinetic energy of the ball as it moves down a length l on the incline if the friction coefficient is half the value calculated in part (a).
What is the difference between sliding and slipping?
A solid spherical ball rolls on an inclined plane without slipping. The ratio of rotational energy and total energy is ______.
