Advertisements
Advertisements
प्रश्न
Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
उत्तर
Yes.
According to Euclid’s 5th postulate, when n line falls on l and m and if
∠1 + ∠2 < 180°, then ∠3 + ∠4 > 180°, producing line l and m further will meet in the side of ∠1 and ∠2 which is less than 180°.
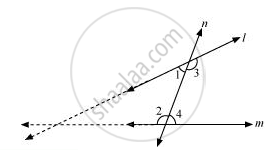
If ∠1 + ∠2 = 180°, then ∠3 + ∠4 = 180°
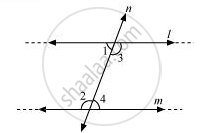
The lines l and m neither meet at the side of ∠1 and ∠2 nor at the side of ∠3 and ∠4. This means that the lines l and m will never intersect each other. Therefore, it can be said that the lines are parallel.
APPEARS IN
संबंधित प्रश्न
How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
Euclidean geometry is valid only for curved surfaces.
Two distinct intersecting lines cannot be parallel to the same line.
Study the following statement:
“Two intersecting lines cannot be perpendicular to the same line”.
Check whether it is an equivalent version to the Euclid’s fifth postulate.
[Hint: Identify the two intersecting lines l and m and the line n in the above statement.]
