Question

Draw a diagram of a combination of three movable pulleys and one fixed pulley to lift up a load. In the diagram, show the directions of load, effort and tension in each strand. Find:

1. mechanical advantage,
2. Velocity ratio and
3. efficiency of the combination in ideal situation.

Answer 1

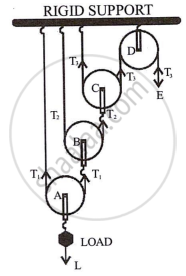
A, B, and C are a movable pulley and D is a fixed pulley.

1. M.A.
   In equilibrium, Effort E = T₃  ...(i)
   

   Since the two string segments that cross pulley A support the load L, tension T₁ in this string is 2T₁ = L.
   or T₁ = `L/2`  ...(ii)
   Similar to how the two sections of string that cross pulley B support tension T₁, tension T₂ in this string is
   `2T_2 = T_1 or T_2 = T_1/2 = L/2^2`  ...(iii)

   Likewise, the string tension T₃ that crosses the pulley C is
   `2T_3 = T_2 or T_3 = T_2/2 = L/2^3`  ...(iv)
   from (iv)
   Load L = `2^3 xx T_3`  ...(v)
   E = `L/2^3`  ...(vi)
   Hence, mechanical advantage
   M.A = `"Load L"/ "effort E"`
   = `(2^2 xx T_3)/T_3 = 2^3`  ...(vii)
   Generally speaking, if there are n movable pulleys and 1 fixed pulley.
   M.A = 2ⁿ here n = 3
   ∴M.A. = 2³  ...(i)

2. Velocity Ratio: When a string crosses a movable pulley, its other end travels up twice as far as the pulley's axle moves. This is because one end of the string is stationary. If the load L attached to the pulley A moves up by distance X i.e. d_L = X, the string connected to the axle of pulley B moves up by a distance 2 × x = 2x, the string connected to the axle of pulley c moves up by a distance 2 × 2x = 2² x and the end of the string moving over the fixed pulley D moves up by a distance 2 × 2² x = 2³ x, i.e. the effort E moves by a distance 2³x or d_E = 2³ x
   ∴ Velocity Ratio V.R. = `("distance moved by effort"  d_E)/("distance moved by load"  d_L)`
   = `(2^3x)/(x) = 2^3`  ...(ii)

3. Efficiency = `("M.A.")/("V.R.")`     ...from (i) and (ii)
   η = `2^3/2^3 = 1 or 100%`