Advertisements
Advertisements
प्रश्न
Draw a line segment AB of 4 cm in length. Draw a line perpendicular to AB through A and B, respectively. Are these lines parallel?
उत्तर
Given: A line segment AB of length 4 cm.
To construct: To draw a line perpendicular to AB through A and B, respectively.
Use the following steps of construction.
1. Draw AB = 4 cm.
2. With 4 as centre and radius more than `1/2` AB, draw an arc that is intersect AB at E.
3. With E as centre and with same radius as above draw an arc which intersect previous arc at F.
4. Again, taking F as centre and with same radius as above draw an arc which intersect previous arc (obtained in step ii) at G.
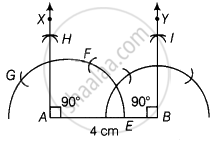
5. With G and F are centres, draw arcs which intersect each other at H.
6. Join AH. So, AX is perpendicular to AB at A. Similarly, draw BY ⊥ AB at B.
Now, we know that if two lines are parallel, then the angle between them will be 0° or 180°.
So, ∠XAB = 90° ...[XA ⊥ AB]
And ∠YBA = 90° ...[YB ⊥ AB]
∠XAB + ∠YBA = 90° + 90° = 180°
Hence, the lines XA and YS are parallel. ...[It sum of interior angle on same side of transversal is 180°, then the two lines are parallel]
APPEARS IN
संबंधित प्रश्न
Construct the angles of the following measurement:- 30°
Construct the 75° angles and verify by measuring it by a protractor.
Construct the 135° angles and verify by measuring it by a protractor.
Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line.
Using ruler and compasses only, draw a right angle.
Construct the angle of the measurement:
1. 135°
Construct a rectangle whose adjacent sides are of lengths 5 cm and 3.5 cm.
