Advertisements
Advertisements
प्रश्न
Draw an acute angled Δ PQR. Draw all of its altitudes. Name the point of concurrence as ‘O’.
उत्तर

Steps of construction:
- Draw any acute angled ∆ PQR.
- With P as centre, draw an arc that cut the side QR at X and Y.
- With X as centre and radius more than half of XY, draw an arc below QR. With Y as centre and same radius draw another arc that cut the previous arc at A.
- Join PA that intersects QR at L. So, PL is the altitude on side QR.
In the same manner, draw QM⊥PR and RN⊥PQ.
Hence, ∆PQR is the required triangle with altitudes PL, QM and RN on sides QR, RP and PQ respectively, with O as the point of concurrence of all the three altitudes.
संबंधित प्रश्न
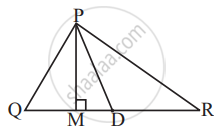
In ΔPQR, D is the mid-point of `bar(QR)`.
`bar(PM)` is ______.
PD is ______.
Is QM = MR?
Draw rough sketch for the following:
In ΔABC, BE is a median.
Draw rough sketch for the following:
In ΔPQR, PQ and PR are altitudes of the triangle.
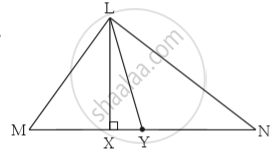
In Δ LMN, _____ is an altitude and _____ is a median. (write the names of appropriate segments.)
Draw a right angled Δ XYZ. Draw its medians and show their point of concurrence by G.
Name the orthocentre of ∆PQR
The triangle ABC formed by AB = 5 cm, BC = 8 cm, AC = 4 cm is ______.
How many altitudes does a triangle have?
The ______ triangle always has altitude outside itself.
Median is also called ______ in an equilateral triangle.
