Advertisements
Advertisements
प्रश्न
Draw an angle of 60° using ruler and compasses and divide it into four equal parts. Measure each part.
उत्तर

Steps of construction:
(i) Draw a ray `vec(OA)`
(ii) With O as centre and any convenient radius draw an arc meeting the rav OA at X.
(iii) With X as centre and the same radius draw an arc which cuts the previously drawn arc at U.
(iv) Join OU and produce it to any point B. So ∠BOA = 60°.
(v) Now with centre X and U and radius more than `1/2(hat(UX))` draw the arcs on the same side of ∠BOA which cuts each other at V.
(vi) Join OV and produce it any point C as well as it cuts the arc `hat(UX)` at W.
(vii) Again with the centre X and W and radius more than `1/2(hat(WX))` draw the arcs on the same side of ∠BOA which cuts each other at Z.
(viii) Join OZ and produce it to any point D.
(ix) With the centre U and W and radius more than `1/2 (hat(UW))` draw the arcs on the same side of ∠BOA with cuts each other at the point P.
(x) Join OP and produce it to any point E. Now with the help of protractor we observe that each angle i.e, ∠BOE = ∠EOC = ∠COD = ∠DOA = 15°.
APPEARS IN
संबंधित प्रश्न
The line of symmetry of a line segment is the ______ bisector of the line segment.
It is possible to draw two bisectors of a given angle.
Infinitely many perpendiculars can be drawn to a given ray.
In figure, the point C is the image of point A in line l and line segment BC intersects the line l at P.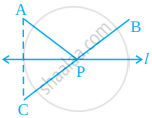
(a) Is the image of P in line l the point P itself?
(b) Is PA = PC?
(c) Is PA + PB = PC + PB?
(d) Is P that point on line l from which the sum of the distances of points A and B is minimum?
Draw an angle of 140° with the help of a protractor and bisect it using ruler and compasses.
Copy figure on your notebook and draw a perpendicular to l through P, using (i) set squares (ii) protractor (iii) ruler and compass. How many such perpendiculars are you able to draw?
Draw a line segment of length 10 cm. Divide it into four equal parts. Measure each of these parts.
Draw the perpendicular bisector of `overline"XY"` whose length is 10.3 cm.
- Take any point P on the bisector drawn. Examine whether PX = PY
-
If M is the midpoint of `overline"XY"`, what can you say about the lengths MX and XY?
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Repeat Question 6, if `overline"AB"` happens to be a diameter.
