Advertisements
Advertisements
प्रश्न
द्विघात बहुपद् x2 + kx + k, k ≠ 0 के शून्यक ______।
पर्याय
दोनों धनात्मक नहीं हो सकते
दोनों ऋणात्मक नहीं हो सकते
सदैव असमान होते है
सदैव बराबर होते है
उत्तर
द्विघात बहुपद् x2 + kx + k, k ≠ 0 के शून्यक दोनों धनात्मक नहीं हो सकते।
स्पष्टीकरण:
स्थिति − 1
`x = (-b ± sqrt(b^2 - 4ac))/(2a)`
द्विघात समीकरण में मूलों को निर्धारित करने के लिए समीकरण में, a, k, b के लिए 1, और k के लिए c मान रखता है |
`x = (−k ± sqrt((k)^2 - 4k))/(2(1))`
=`(−k ± sqrt(k(k - 4)))/2`
इसका मूल होना चाहिए k(k − 4) > 0
स्थिति − 2
के लिए k(k − 4) > 0 सत्य है, या तो।
k < 0
k > 4
स्थिति के लिए,
k < 0
k = −2
x = `-k ± sqrt(k(k - 4))/2`
मान रखते हैा मूल रूप प्राप्त करने के लिए
x = `(-(-2) ± sqrt(-2)(-2 - 4))/2`
= `(2 ± sqrt12)/2`
= `(2 ± 3.46)/2`
एक मूल धनात्मक और एक मूल ऋणात्मक।
इस स्थिति मैं।
k > 4
k = 5
समीकरण में
k = 5 रखते है,
x = `(−k ± sqrt(k(k - 4)))/2` मूलों का मूल स्वरूप प्राप्त करने के लिए। तो,
x = `(-(5) ± sqrt((5)(5 - 4)))/2`
= `(-5 ± sqrt5)/2`
= `(-5 ± 2.236)/2`
दोनों वर्ग ऋणात्मक हैं।
दोनों शर्तों के लिए या, समीकरणों की दोनों मूल k < 0, k > 4 कभी धनात्मक नहीं हो सकते।
APPEARS IN
संबंधित प्रश्न
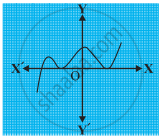
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
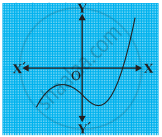
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
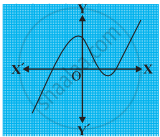
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
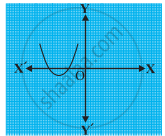
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
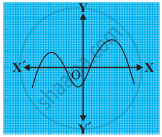
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
यदि द्विधात बहुपद x2 + (a + 1) x + b के शून्यक 2 और –3 हैं, तो
यदि द्विघात बहुपद ax2 + bx + c, c ≠ 0 के शून्यक बराबर हैं, तो ______ ।
निम्नलिखित में से कौन एक द्विघात बहुपद का आलेख नहीं है?
यदि एक बहुपद का आलेख x-अक्ष को केवल एक ही बिंदु पर प्रतिच्छेद करे, तो यह एक द्विघात बहुपद् नहीं हो सकता।
यद् एक बहुपद का आलेख x-अक्ष को ठीक दो बिन्दुओं पर प्रतिच्छेद करता है, तो यह आवश्यक नहीं है कि वह एक द्विधात बहुपद हो।
