Advertisements
Advertisements
प्रश्न
एक चॉकलेट का मूल्य ₹ (x + 4) है तथा रोहित ने (x + 4) चॉकलेट खरीदीं। x के पदों में उसके द्वारा भुगतान की गयी कुल धनराशि ज्ञात कीजिए। यदि x = 10 है, तो उसके द्वारा दी गयी कुल धनराशि ज्ञात कीजिए।
उत्तर
रोहित द्वारा भुगतान की गई कुल राशि का पता लगाएं -
चूंकि, चॉकलेट की मूल्य = x + y है,
रोहित ने खरीदा (x + y) चॉकलेट।
∴ (x + y) चॉकलेट की मूल्य = एक चॉकलेट की मूल्य × चॉकलेट की संख्या
= (x + 4) × (x + 4)
= (x + 4)2
= x2 + 8x + 16
∴ रोहित द्वारा भुगतान की गई कुल राशि = Rs. (x2 + 8x + 16)
x = 10 के लिए भुगतान की गई राशि का पता लगाएंः उपरोक्त चरण से, यह नोट किया जाता है कि, रोहित द्वारा भुगतान की गई कुल राशि = Rs. (x2 + 8x + 16) यदि x = 10 है, तो रोहित द्वारा भुगतान की गई राशि = (10)2 + 8 × 10 + 16 = 100 + 80 + 16 = Rs. 196
इस प्रकार, रोहित द्वारा भुगतान की गई कुल राशि Rs. (x2 + 8x + 16) है और यदि x = 10 है, तो रोहित द्वारा भुगतान की गई राशि Rs. 196 है।
APPEARS IN
संबंधित प्रश्न
उपयुक्त सर्वसमिकाओं का प्रयोग करते हुए, निम्न को प्रसारित कीजिए -
सर्वसमिका a2 + 2ab + b2 = (a + b)2 का प्रयोग करते हुए, निम्न के गुणनखंड कीजिए -
x2 + 12x + 36
सर्वसमिका a2 + 2ab + b2 = (a + b)2 का प्रयोग करते हुए, निम्न के गुणनखंड कीजिए -
x2 + 14x + 49
सर्वसमिका a2 + 2ab + b2 = (a + b)2 का प्रयोग करते हुए, निम्न के गुणनखंड कीजिए -
सर्वसमिका a2 + 2ab + b2 = (a + b)2 का प्रयोग करते हुए, निम्न के गुणनखंड कीजिए -
9x2 + 24x + 16
सर्वसमिका a2 + 2ab + b2 = (a + b)2 का प्रयोग करते हुए, निम्न के गुणनखंड कीजिए -
9x2 + 30x + 25
यदि a2 + b2 = 74 और ab = 35 है, तो a + b ज्ञात कीजिए।
नीचे दिए चित्र में कार्डों को उपयुक्त संख्या में लीजिए जिनमें [G(x × x)] जो x2 निरूपित करता है, R(x × 1) जो x निरूपित करता है तथा Y(1 × 1) जो 1] निरूपित करता है। इन कार्डों को आयतों के रूप में व्यवस्थित करके निम्न व्यंजकों के गुणनखंड कीजिए -
- 2x2 + 6x + 4
- x2 + 4x + 4
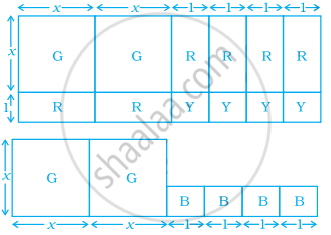
उपरोक्त आकृति का क्षेत्रफल परिकलित कौजिए।
