Advertisements
Advertisements
प्रश्न
Equations of pairs of opposite sides of a parallelogram are x2 - 7x + 6 = 0 and y2 − 14y + 40 = 0. Find the joint equation of its diagonals.
उत्तर
Let ABCD be the parallelogram such that the combined equation of sides AB and CD is x2 - 7x + 6 = 0 and the combined equation of sides BC and AD y2 - 14y + 40 = 0
The separate equations of the lines represented by x2 - 7x + 6 = 0, i.e. (x - 1)(x - 6) = 0 are x - 1 = 0 and x - 6 = 0
Let equation of the side AB be x - 10 and equation of side CD be x - 6 = 0
The separate equations of the lines represented by y2 - 14y + 40 = 0, i.e. (y - 4)(y - 10) = 0 are y - 4 = 0 and y - 10 = 0
Let equation of the side BC be y - 4 = 0 and equation of side AD be y - 10 = 0
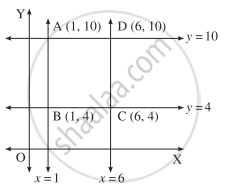
Coordinates of the vertices of the parallelogram are A(1, 10), B(1, 4), C(6, 4) and D(6, 10)
∴ equation of the diagonal AC is
`("y" - 10)/("x" - 1) = (10 - 4)/(1 - 6) = 6/-5`
∴ 5y + 50 = 6x − 6
∴ 6x + 5y − 56 = 0
and equation of the diagonal BD is
`("y" - 4)/("x" - 1) = (4 - 10)/(1 - 6) = (-6)/-5 = 6/5`
∴ 5y - 20 = 6x - 6
∴ 6x - 5y + 14 = 0
Hence, the equations of the diagonals are 6x + 5y - 56 = 0 and 6x - 5y + 14 = 0
∴ the joint equation of the diagonals is
(6x + 5y - 56)(6x - 5y + 14) = 0
∴ `36"x"^2 - 30"xy" + 84"x" + 30"xy" - 25"y"^2 + 70"y" - 336"x" + 280"y" - 784 = 0`
∴ `36"x"^2 - 25"y"^2 - 252"x" + 350"y" - 784 = 0`
[Note: Answer in the textbook is incorrect]
APPEARS IN
संबंधित प्रश्न
Find p and q if the equation px2 – 8xy + 3y2 + 14x + 2y + q = 0 represents a pair of prependicular lines.
Find the joint equation of the pair of the line through the point (2, -1) and parallel to the lines represented by 2x2 + 3xy - 9y2 = 0.
Find the joint equation of the pair of the line through the point (2, -3) and parallel to the lines represented by x2 + xy - y2 = 0.
Show that the equation x2 + 2xy + 2y2 + 2x + 2y + 1 = 0 does not represent a pair of lines.
Show that the equation 2x2 - xy - 3y2 - 6x + 19y - 20 = 0 represents a pair of lines.
Show that the equation 2x2 + xy - y2 + x + 4y - 3 = 0 represents a pair of lines. Also, find the acute angle between them.
Find the separate equation of the line represented by the following equation:
(x - 2)2 - 3(x - 2)(y + 1) + 2(y + 1)2 = 0
Find the value of k, if the following equations represent a pair of line:
3x2 + 10xy + 3y2 + 16y + k = 0
Find the value of k, if the following equations represent a pair of line:
kxy + 10x + 6y + 4 = 0
Find the value of k, if the following equations represent a pair of line:
x2 + 3xy + 2y2 + x - y + k = 0
Find the separate equation of the line represented by the following equation:
10(x + 1)2 + (x + 1)(y - 2) - 3(y - 2)2 = 0
Find the coordinates of the points of intersection of the lines represented by x2 − y2 − 2x + 1 = 0
Find k, if the slopes of lines given by kx2 + 5xy + y2 = 0 differ by 1.
The point of intersection of lines given by the equation 2x2 + 4xy - 2y2 + 4x + 8y + 1 = 0 is ______
If the slope of one of the lines given by ax2 + 2hxy + by2 = 0 is two times the other, then ______
If (a + 3b)(3a + b) = 4h2, then the angle between the lines represented by ax2 + 2hxy + by2 = 0 is ______
If the equation `lambdax^2 + 2y^2 - 5xy + 5x - 7y + 3 = 0` represents two straight lines, then the value of λ will be ______.
If ax2 + 2xy – 3y2 + 4x + c = 0 represents a pair of perpendicular lines, then ______.
Equation of line passing through the points (0, 0, 0) and (2, 1, –3) is ______.
The point of intersection of line represented by x2 – y2 + 3y – 2 = 0 is ______.
ΔOAB is formed by lines x2 – 4xy + y2 = 0 and the line x + y – 2 = 0. Find the equation of the median of the triangle drawn from O.
Find the coordinates of the point of intersection of the pair of lines 6x2 + 5xy – 4y2 + 7x + 13y – 3 = 0.
Find the point of intersection of the lines given by x2 + 3xy + 2y2 + x – y – 6 = 0
Find the values of p and q if the equation px2 – 6xy + y2 + 18x – qy + 8 = 0 represents a pair of parallel lines.
