Advertisements
Advertisements
प्रश्न
Explain in detail the thermal expansion.
उत्तर
Thermal expansion is the tendency of matter to change in shape, area, and volume due to a change in temperature.
All three states of matter (solid, liquid and gas) expand when heated. When a solid is heated, its atoms vibrate with a higher amplitude about their fixed points. The relative change in the size of solids is small. Railway tracks are. given small gaps so that in the summer, the tracks expand and do not buckle. Railroad tracks and bridges have expansion joints to allow them to expand and contract freely with temperature changes.

Liquids have less intermolecular forces than solids and hence they expand more than solids. This is the principle behind mercury thermometers.
In the case of gas molecules, the intermolecular forces are almost negligible and hence they expand much more than solids. For example in hot air balloons when gas particles get heated, they expand and take up more space.
The increase in dimension of a body due to the increase in its temperature is called thermal expansion.
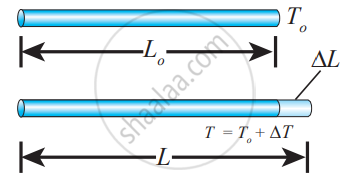
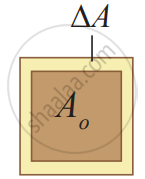
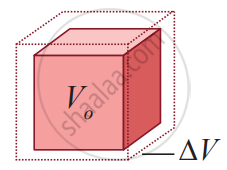
The expansion in length is called linear expansion. Similarly, the expansion in area is termed as area expansion and the expansion in volume is tanned as volume expansion.
Linear expansion
Area expansion
Volume expansion
Linear Expansion: In solids, for a small change in temperature ∆T, the fractional change in length `((Δ"L")/("L"_0))` is directly proportional to ∆T.
`(Δ"L")/("L"_0) = α_"L"Δ"T"`
Therefore, `α_"L" = (Δ"L")/("L"_0Δ"T")`
Where, αL = coefficient of linear expansion,
∆L = Change in length,
L = Original length,
∆T = Change in temperature.
Area Expansion: For a small change in temperature ∆T the fractional change in the area `((Δ"A")/("A"_0))` of a substance is directly proportional to ∆T and it can be written as
`(Δ"A")/("A"_0) = α_"A"Δ"T"`
Therefore, `α_"A" = (Δ"A")/("A"_0Δ"T")`
Where, αA = coefficient of area expansion.
∆A = Change in area,
A = Original area,
∆T = Change in temperature.
Volume Expansion: For a small change in temperature AT the fractional change in the volume `((Δ"V")/("V"_0))` of a substance is directly proportional to ∆T.
`(Δ"V")/("V"_0) = α_"V"Δ"T"`
Therefore, `α_"V" = (Δ"V")/("V"_0Δ"T")`
Where, αv = coefficient of volume expansion,
∆V = Change in volume,
V = Original volume,
∆T = Change in temperature,
Unit of coefficient of the linear, area and volumetric expansion of solids is °C-1 or K-1
APPEARS IN
संबंधित प्रश्न
Choose the correct option.
A glass bottle completely filled with water is kept in the freezer. Why does it crack?
Choose the correct option.
Consider the following statements-
(I) The coefficient of linear expansion has dimension K-1.
(II) The coefficient of volume expansion has dimension K-1.
Choose the correct option.
Water falls from a hight of 200 m. What is the difference in temperature between the water at the top and bottom of a waterfall given that the specific heat of water is 4200 J kg-1 °C-1?
Obtain an ideal gas law from Boyle’s and Charles’ law.
Write the unit of specific heat capacity.
What is a thermal expansion?
Give the expression for linear thermal expansion.
Give the expression for volume thermal expansion.
Discuss various modes of heat transfer.
The temperature of a uniform rod of length L having a coefficient of linear expansion αL is changed by ∆T. Calculate the new moment of inertia of the uniform rod about the axis passing through its center and perpendicular to an axis of the rod.
