Advertisements
Advertisements
प्रश्न
Explain the concepts of fundamental frequency, harmonics and overtones in detail.
उत्तर
Fundamental frequency and overtones: Let us now keep the rigid boundaries at x = 0 and x = L and produce standing waves by wiggling the string (as in plucking strings in a guitar). Standing waves with a specific wavelength are produced. Since, the amplitude must vanish at the boundaries, therefore, the displacement at the boundary must satisfy the following conditions
x(x = 0, t) = 0 and y(x = L, t) = 0
Since, the nodes formed at a distance
where n is an integer, L is the length between the two boundaries and λn is the specific wavelength that satisfy the specified boundary conditions. Hence,
Therefore, not all wavelengths are allowed. The (allowed) wavelengths should fit with the specified boundary conditions, i.e., for n = 1, the first mode of vibration has a specific wavelength λ1 = 2L. Similarly for n = 2, the second mode of vibration has a specific wavelength
For n = 3, the third mode of vibration has specific wavelength
The frequency of each mode of vibration (called natural frequency) can be calculated.
We have,
The lowest natural frequency is called the fundamental frequency.
The second natural frequency is called the first over tone.
The third natural frequency is called the second over tone.
Therefore, the nth natural frequency can be computed as integral (or integer ) multiple of the fundamental frequency, i.e.,
fn = nf1 where n is an integer …(5)
If natural frequencies are written as an integral multiple of fundamental frequencies, then the frequencies are called harmonics. Thus, the first harmonic is f1 = f1 (the fundamental frequency is called first harmonic), the second harmonic is f2 = 2f1, the third harmonic is f3 = 3f1 etc.
APPEARS IN
संबंधित प्रश्न
For a particular tube, among six harmonic frequencies below 1000 Hz, only four harmonic frequencies are given: 300 Hz, 600 Hz, 750 Hz and 900 Hz. What are the two other frequencies missing from this list?
Let y =
change during propagation. The velocity of the wave is:
What is a stationary wave?
Explain the formation of stationary waves.
Write the characteristics of stationary waves.
Discuss the law of transverse vibrations in stretched strings.
What is a sonometer? Give its construction and working. Explain how to determine the frequency of tuning fork using a sonometer.
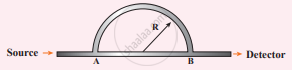
A sound wave is transmitted into a tube as shown in the figure. The sound wave splits into two waves at point A which recombine at point B. Let R be the radius of the semi-circle which is varied until the first minimum. Calculate the radius of the semi-circle if the wavelength of the sound is 50.0 m.
Police in a siren car moving with a velocity 20 ms– chases a thief who is moving in a car with a velocity v0 ms-1. The police car sounds at frequency 300 Hz, and both of them move towards a stationary siren of frequency 400 Hz. Calculate the speed in which thief is moving. (Assume the thief does not observe any beat)
