Advertisements
Advertisements
प्रश्न
Factorise the following expressions
m2 + m – 72
उत्तर
m2 + m – 72
This is of the form ax + bx + c
where a = 1, b = 1, c = – 72
| Product = – 72 | Sum = 1 |
| 1 × (– 72) = – 72 | 1 + (– 72) = – 71 |
| 2 × (– 36) = – 72 | 2 + (– 36) = – 34 |
| 3 × (– 24) = – 72 | 3 + (– 24) = – 21 |
| 4 × (– 18) = – 72 | 4 + (– 18) = – 14 |
| 6 × (– 12) = – 72 | 6 + (– 12) = – 6 |
| 8 × (– 9) = – 72 | 8 + (– 9) = – 1 |
| 9 × (– 8) = – 72 | 9 + (– 8) = 1 |
Product a × c = 1 × – 72 = – 72
Sum b = 1
The middle term m can be written as 9m – 8m
m2 + m – 72 = m2 + 9m – 8m – 72
= m(m + 9) – 8(m + 9)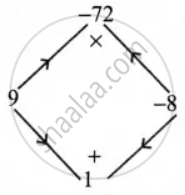
Taking out (m + 9)
= (m + 9)(m – 8)
∴ m2 + m – 72 = (m + 9)(m – 8)
APPEARS IN
संबंधित प्रश्न
Choose the right answers from the option:
The difference of the squares, (612 – 512 ) is equal to ______.
Using the identity (a + b)(a – b) = a2 – b2, find the following product
(p + 2)(p – 2)
Factorise the following algebraic expression by using the identity a2 – b2 = (a + b)(a – b)
9 – 4y2
a2 – b2 = (a + b) ______.
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
4x2 – 25y2
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
p5 – 16p
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
16x4 – 81
Factorise the expression and divide them as directed:
(3x2 – 48) ÷ (x – 4)
Verify the following:
(ab + bc)(ab – bc) + (bc + ca)(bc – ca) + (ca + ab)(ca – ab) = 0
Find the value of a, if 9a = 762 – 672
