Advertisements
Advertisements
प्रश्न
Factorize the following expressions:
( x + 2)3 + ( x - 2)3
उत्तर
`= (x + 2 + x - 2)((x + 2^2 -(x + 2)(x - 2) + (x - 2)^2) [∵ a^3 + b^3 = (a + b)(a^2 - ab + b^2)]`
`= 2x(x^2 + 4x + 4 - (x + 2)(x - 2) + x^2 - 4x + 4) [∵ (a + b)^2 = a^2 + 2ab + b^2, (a - b)^2 = a^2 - 2ab + b^2]`
`= 2x (2x^2 + 8 - (x^2 - 2^2))` `[∵ (a + b)(a - b) = a^2 - b^2]`
`=2x(2x^2 + 8 - x^2 + 4)`
`= 2x(x^2 + 12)`
`∴ (x + 2)^3 + (x - 2)^3 = 2x(x^2 + 12)`
APPEARS IN
संबंधित प्रश्न
Factorize : x2 + y - xy - x
Factorize `x^2 - 2sqrt2x - 30`
Factorize `2x^2 - 5/6x + 1/12`
`3sqrt3a^3 - b^3 - 5sqrt5c^3 - 3sqrt15abc`
If x2 + y2 = 29 and xy = 2, find the value of x + y.
Write the value of 483 − 303 − 183.
Mark the correct alternative in each of the following: The factors of a2 − 1 − 2x − x2 are
Evaluate: (c + 5)(c - 3)
Evaluate: - 4y (15 + 12y - 8z) (x - 2y)
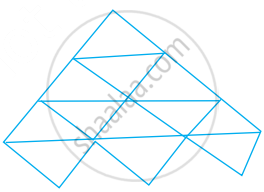
A triangle is made up of 2 red sticks and 1 blue sticks 
. The length of a red stick is given by r and that of a blue stick is given by b. Using this information, write an expression for the total length of sticks in the pattern given below:
