Advertisements
Advertisements
प्रश्न
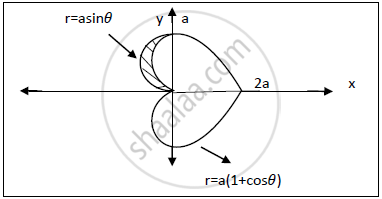
Find the area inside the circle r=a sin𝜽 and outside the cardioide r=a(1+cos𝜽 )
उत्तर
Intersection of cardioide and circle is,
r=a(1+cos𝜽) and r=asin𝜽
asin𝜽 = a(1+cos𝜽) => 𝜽=𝟗𝟎°
a(1+cos𝜽) ≤ r ≤ asin𝜽
`pi/2`≤ 𝜽 ≤ 𝝅
Area of region bounded by given circle and cardioide ,
I = `int_(pi/2)^pi int_(asintheta)^(a(1+costheta)) rdrd theta`
`=int_(pi/2)^pi a^2/2(sin^2theta-1-2costheta-cos^2theta)d theta`
`=int_(pi/2)^pi a^2/2(-1-2costheta-cos^2theta)d theta`
`=a^2/a[-theta-2sintheta-(sin2theta)/2]_(pi/2)^pi`
I =`a^2/2[(-pi-0-0)-(-pi/2-2-0)]`
Required area is = I = `a^2/2(2-pi/2)`
APPEARS IN
संबंधित प्रश्न
Evaluate `int int xy(x-1)dx dy` over the region bounded by 𝒙𝒚 = 𝟒,𝒚= 𝟎,𝒙 =𝟏 and 𝒙 = 𝟒
Evaluate `int int(2xy^5)/sqrt(x^2y^2-y^4+1)dxdy`, where R is triangle whose vertices are (0,0),(1,1),(0,1).
Use polar co ordinates to evaluate `int int (x^2+y^2)^2/(x^2y^2)` 𝒅𝒙 𝒅𝒚 over yhe area Common to circle `x^2+y^2=ax "and" x^2+y^2=by, a>b>0`
Find by double integration the area bounded by the parabola 𝒚𝟐=𝟒𝒙 And 𝒚=𝟐𝒙−𝟒
