Question

Find the area inside the circle r=a sin𝜽 and outside the cardioide r=a(1+cos𝜽 )

Answer 1

Intersection of cardioide and circle is,
r=a(1+cos𝜽) and r=asin𝜽

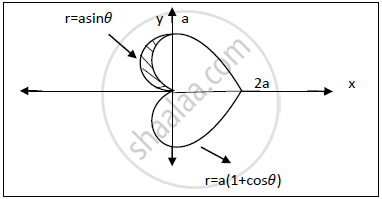
asin𝜽 = a(1+cos𝜽) => 𝜽=𝟗𝟎°
a(1+cos𝜽) ≤ r ≤ asin𝜽

`pi/2`≤ 𝜽 ≤ 𝝅

Area of region bounded by given circle and cardioide ,

I = `int_(pi/2)^pi int_(asintheta)^(a(1+costheta)) rdrd theta`

`=int_(pi/2)^pi a^2/2(sin^2theta-1-2costheta-cos^2theta)d theta`

`=int_(pi/2)^pi a^2/2(-1-2costheta-cos^2theta)d theta`

`=a^2/a[-theta-2sintheta-(sin2theta)/2]_(pi/2)^pi`

I =`a^2/2[(-pi-0-0)-(-pi/2-2-0)]`

Required area is = I = `a^2/2(2-pi/2)`