Advertisements
Advertisements
प्रश्न
Find the cartesian form of the equation of the plane `bar r=(hati+hatj)+s(hati-hatj+2hatk)+t(hati+2hatj+hatj)`
उत्तर
The equation `barr=bara+sbarb+tbarc` represents a plane passing through a point having position vector a and parallel to the vectors b and c .
Here, `bara=hati+hatj, barb=hati-hatj+2hatk and barc=hati+2hatj+hatk`
The given plane is perpendicular to the vector `barn`
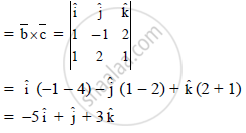
Vector equation of the plane in scalar product form is `barr.barn=bara.barn`
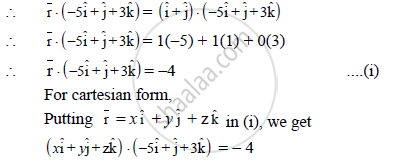
`therefore x(-5)+y(1)+z(3)=-4`
`therefore -5x+y+3z=-4`
`therefore 5x-y-3z=4`
which is the cartesian form of the equation of the plane
APPEARS IN
संबंधित प्रश्न
Find the vector equation of the plane passing through a point having position vector `3 hat i- 2 hat j + hat k` and perpendicular to the vector `4 hat i + 3 hat j + 2 hat k`
Find the vector equation of the plane which is at a distance of 5 units from the origin and which is normal to the vector `2hati + hatj + 2hatk.`
Parametric form of the equation of the plane is `bar r=(2hati+hatk)+lambdahati+mu(hat i+2hatj+hatk)` λ and μ are parameters. Find normal to the plane and hence equation of the plane in normal form. Write its Cartesian form.
Find the vector equation of the plane with intercepts 3, –4 and 2 on x, y and z-axis respectively.
Find the Cartesian equation of the following planes:
`vecr.(2hati + 3hatj-4hatk) = 1`
Find the Cartesian equation of the following planes:
`vecr.[(s-2t)hati + (3 - t)hatj + (2s + t)hatk] = 15`
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
2x + 3y + 4z – 12 = 0
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
x + y + z = 1
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
5y + 8 = 0
Find the vector and Cartesian equation of the planes that passes through the point (1, 0, −2) and the normal to the plane is `hati + hatj - hatk`
The Cartesian equation of the line is 2x - 3 = 3y + 1 = 5 - 6z. Find the vector equation of a line passing through (7, –5, 0) and parallel to the given line.
Find the image of a point having the position vector: `3hati - 2hatj + hat k` in the plane `vec r.(3hati - hat j + 4hatk) = 2`
Find the vector and Cartesian equations of the line passing through (1, 2, 3) and parallel to the planes \[\vec{r} \cdot \left( \hat{i} - \hat{j} + 2 \hat{k} \right) = 5 \text{ and } \vec{r} \cdot \left( 3 \hat{i} + \hat{j} + 2 \hat{k} \right) = 6\]
Find the vector and Cartesian forms of the equation of the plane passing through the point (1, 2, −4) and parallel to the lines \[\vec{r} = \left( \hat{i} + 2 \hat{j} - 4 \hat{k} \right) + \lambda\left( 2 \hat{i} + 3 \hat{j} + 6 \hat{k} \right)\] and \[\vec{r} = \left( \hat{i} - 3 \hat{j} + 5 \hat{k} \right) + \mu\left( \hat{i} + \hat{j} - \hat{k} \right)\] Also, find the distance of the point (9, −8, −10) from the plane thus obtained.
Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes \[\vec{r} \cdot \left( \hat{i} - \hat{j} + 2 \hat{k} \right) = 5 \text{ and } \vec{r} \cdot \left( 3 \hat{i} + \hat{j} + \hat{k} \right) = 6 .\]
Find the vector and cartesian equations of the plane passing throuh the points (2,5,- 3), (-2, - 3,5) and (5,3,-3). Also, find the point of intersection of this plane with the line passing through points (3, 1, 5) and (–1, –3, –1).
Find the Cartesian equation of the plane, passing through the line of intersection of the planes `vecr. (2hati + 3hatj - 4hatk) + 5 = 0`and `vecr. (hati - 5hatj + 7hatk) + 2 = 0` intersecting the y-axis at (0, 3).
Vector equation of a line which passes through a point (3, 4, 5) and parallels to the vector `2hati + 2hatj - 3hatk`.
Find the vector and Cartesian equations of the plane passing through the points (2, 2 –1), (3, 4, 2) and (7, 0, 6). Also find the vector equation of a plane passing through (4, 3, 1) and parallel to the plane obtained above.
Find the vector equation of the plane that contains the lines `vecr = (hat"i" + hat"j") + λ (hat"i" + 2hat"j" - hat"k")` and the point (–1, 3, –4). Also, find the length of the perpendicular drawn from the point (2, 1, 4) to the plane thus obtained.
The vector equation of the line `(x - 5)/3 = (y + 4)/7 = (z - 6)/2` is ______.
The vector equation of the line through the points (3, 4, –7) and (1, –1, 6) is ______.
The Cartesian equation of the plane `vec"r" * (hat"i" + hat"j" - hat"k")` = 2 is ______.
The vector equation of the line `(x - 5)/3 = (y + 4)/7 = (z - 6)/2` is `vec"r" = 5hat"i" - 4hat"j" + 6hat"k" + lambda(3hat"i" + 7hat"j" + 2hat"k")`.
Find the vector and the cartesian equations of the plane containing the point `hati + 2hatj - hatk` and parallel to the lines `vecr = (hati + 2hatj + 2hatk) + s(2hati - 3hatj + 2hatk)` and `vecr = (3hati + hatj - 2hatk) + t(hati - 3hatj + hatk)`
