Advertisements
Advertisements
प्रश्न
Find the number of side of a regular polygon, when of its angle has a measure of 150° .
उत्तर
\[ \text{ Each interior angle } = \left( \frac{2n - 4}{n} \times 90 \right)^° \]
\[So, \left( \frac{2n - 4}{n} \times 90 \right)^° = 150° \]
\[ \Rightarrow \frac{2n - 4}{n} = \frac{150° }{90° }\]
\[ \Rightarrow \frac{2n - 4}{n} = \frac{5}{3}\]
\[ \Rightarrow 6n - 12 = 5n\]
\[ \therefore n = 12\]
APPEARS IN
संबंधित प्रश्न
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
| Figure | 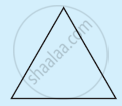 |
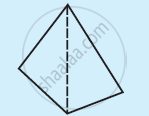 |
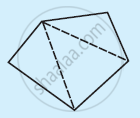 |
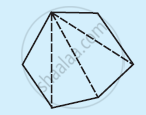 |
| Side | 3 | 4 | 5 | 6 |
| Angle sum | 180° |
2 × 180° = (4 − 2) × 180° |
3 × 180° = (5 − 2) × 180° |
4 × 180° = (6 − 2) × 180° |
What can you say about the angle sum of a convex polygon with number of sides?
a) 7
b) 8
c) 10
d) n
What is a regular polygon?
How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Following are some figures: Classify each of these fugures on the basis of the following:
(i) Simple curve
(ii) Simple closed curve
(iii) Polygon
(iv) Convex polygon
(v) Concave polygon
(vi) Not a curve

State the name of a regular polygon of 6 sides.
Find the number of degrees in each exterior exterior angle of a regular pentagon.
The name of three-sided regular polygon is ______.
A polygon having 10 sides is known as ______.
 is a polygon.
is a polygon.
If the sum of interior angles is double the sum of exterior angles taken in an order of a polygon, then it is a hexagon.
