Advertisements
Advertisements
प्रश्न
Find the smallest number by which the given number must be divided so that the resulting number is a perfect square:
2904
उत्तर
For question, factorise the number into its prime factor.
2904 = 2 x 2 x 2 x 3 x 11 x 11
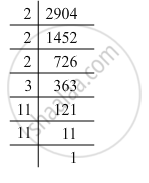
Grouping the factors into pairs:
2904 = (2 x 2) x (11 x 11) x 2 x 3
Here, the factors 2 and 3 do not occur in pairs. To be a perfect square, all the factors have to be in pairs. Hence, the smallest number by which 2904 must be divided for it to be a perfect square is 2 x 3, i.e. 6.
APPEARS IN
संबंधित प्रश्न
Find the smallest square number that is divisible by each of the numbers 8, 15, and 20.
Find the smallest number by which the given number must be divided so that the resulting number is a perfect square:
14283
Write five numbers for which you cannot decide whether they are squares.
Write true (T) or false (F) for the following statement.
There are fourteen square number upto 200.
Find the square root the following by prime factorization.
47089
Find the square root the following by prime factorization.
27225
A school collected Rs 2304 as fees from its students. If each student paid as many paise as there were students in the school, how many students were there in the school?
Find the least square number, exactly divisible by each one of the numbers:
(i) 6, 9, 15 and 20
Find the square root by prime factorisation method
4761
Using prime factorisation, find the square roots of 11025
