Advertisements
Advertisements
Question
Find the smallest number by which the given number must be divided so that the resulting number is a perfect square:
2904
Advertisements
Solution
For question, factorise the number into its prime factor.
2904 = 2 x 2 x 2 x 3 x 11 x 11
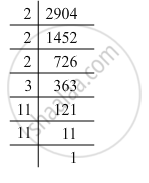
Grouping the factors into pairs:
2904 = (2 x 2) x (11 x 11) x 2 x 3
Here, the factors 2 and 3 do not occur in pairs. To be a perfect square, all the factors have to be in pairs. Hence, the smallest number by which 2904 must be divided for it to be a perfect square is 2 x 3, i.e. 6.
APPEARS IN
RELATED QUESTIONS
For the following number, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
2028
For the following number, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
768
Find the square root the following by prime factorization.
24336
Find the smallest number by which 147 must be multiplied so that it becomes a perfect square. Also, find the square root of the number so obtained.
A welfare association collected Rs 202500 as donation from the residents. If each paid as many rupees as there were residents, find the number of residents.
A school collected Rs 2304 as fees from its students. If each student paid as many paise as there were students in the school, how many students were there in the school?
Find the square roots of 121 and 169 by the method of repeated subtraction.
Write the prime factorization of the following number and hence find their square root.
7744
Find the square root by prime factorisation method
4761
