Advertisements
Advertisements
प्रश्न
Find the sum (−5) + (−8)+ (−11) + ... + (−230) .
उत्तर
(−5) + (−8)+ (−11) + ... + (−230) .
Common difference of the A.P. (d) = a2 - a1
=-8-(-5)
=-8+5
=-3
So here,
First term (a) = −5
Last term (l) = −230
Common difference (d) = −3
So, here the first step is to find the total number of terms. Let us take the number of terms as n.
Now, as we know,
an = a + (n-1) d
So, for the last term,
- 230 = -5 + ( n-1) (-3)
- 230 = -5-3n + 3
-23 +2 = -3n
`(-228)/(-3) = n`
n = 76
Now, using the formula for the sum of n terms, we get
`S_n = 76/2 [2(-5) + (76-1) (-3)]`
= 38 [-10+(75)(-3)]
=38 (-10-225)
= 38(-235)
= -8930
Therefore, the sum of the A.P is Sn = -8930
APPEARS IN
संबंधित प्रश्न
The sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
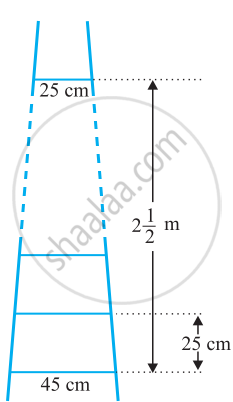
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
How many numbers are there between 101 and 999, which are divisible by both 2 and 5?
Find the sum of the first 15 terms of each of the following sequences having nth term as xn = 6 − n .
The first and last terms of an A.P. are 1 and 11. If the sum of its terms is 36, then the number of terms will be
If the sums of n terms of two arithmetic progressions are in the ratio \[\frac{3n + 5}{5n - 7}\] , then their nth terms are in the ratio
Find the common difference of an A.P. whose first term is 5 and the sum of first four terms is half the sum of next four terms.
Write the formula of the sum of first n terms for an A.P.
The sum of 41 terms of an A.P. with middle term 40 is ______.
k + 2, 2k + 7 and 4k + 12 are the first three terms of an A.P. The first term of this A.P. is ______.
