Advertisements
Advertisements
प्रश्न
Find the sum of all integers between 50 and 500, which are divisible by 7.
उत्तर
In this problem, we need to find the sum of all the multiples of 7 lying between 50 and 500.
So, we know that the first multiple of 7 after 50 is 56 and the last multiple of 7 before 500 is 497.
Also, all these terms will form an A.P. with the common difference of 7.
So here,
First term (a) = 56
Last term (l) = 497
Common difference (d) = 7
So, here the first step is to find the total number of terms. Let us take the number of terms as n.
Now, as we know,
`a-n = a+ (n -1)d`
So, for the last term,
497 = 56 + (n -1)7
497 = 56+ 7n - 7
497 = 49 +7n
497 - 49 = 7n
Further simplifying
448 = 7n
`n = 448/7`
n = 64
Now, using the formula for the sum of n terms,
`S_n = n/2 [2a + (n -1)d]`
For n = 64 we get
`S_n = 64/2 [2(56) + (64 - 1) 7]`
= 32 [112 + (63)7]
= 32(1123 + 441)
= 32(112 + 441)
= 32(553)
= 17696
Therefore the sum of all the multiples of 7 lying betwenn 50 and 500 is `S_n = 17696`
APPEARS IN
संबंधित प्रश्न
Ramkali required Rs 2,500 after 12 weeks to send her daughter to school. She saved Rs 100 in the first week and increased her weekly saving by Rs 20 every week. Find whether she will be able to send her daughter to school after 12 weeks.
What value is generated in the above situation?
Find the sum of the following APs:
2, 7, 12, ..., to 10 terms.
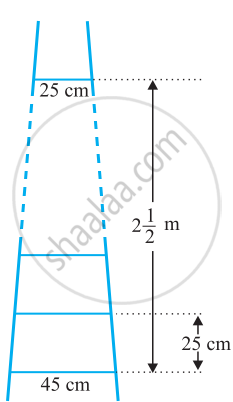
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
The first term of an AP is p and its common difference is q. Find its 10th term.
Find the sum of all multiples of 9 lying between 300 and 700.
If the sum of n terms of an A.P. is 2n2 + 5n, then its nth term is
The sum of first n odd natural numbers is ______.
If \[\frac{5 + 9 + 13 + . . . \text{ to n terms} }{7 + 9 + 11 + . . . \text{ to (n + 1) terms}} = \frac{17}{16},\] then n =
Shubhankar invested in a national savings certificate scheme. In the first year he invested ₹ 500, in the second year ₹ 700, in the third year ₹ 900 and so on. Find the total amount that he invested in 12 years
The sum of the first 15 multiples of 8 is ______.
