Advertisements
Advertisements
प्रश्न
Find the area bounded by the curve y = x2 and the line y = 4.
उत्तर
Equation of the curve y = x2 ...(1)
Equation of the line y = 4 ...(2)
Solving equation (1) and (2)
x2 = 4
⇒ x = ± 2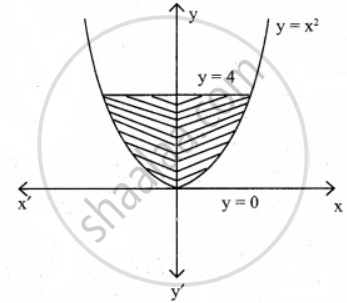
Required Area
A = `int_(-2)^2 y_1 "d"x - int_(-2)^2 y_2 "d"x`
= `int_(-2)^2 4"d"x - int_(-2)^2 x^"d"x`
= `[4x]_(-2)^2 - [x^3/3]_(-2)^2`
= `[4(2) - 4(-2)] - [(2)^3/3 - (-2)^3/3]`
= `(8 + 8) - (8/3 + 8/3)`
= `16 - 16/3`
= `16[1 - 1/3]`
= `16(2/3)`
= `32/3` sq.units
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the lines y – 2x – 4 = 0, y = 0, y = 3 and the y-axis
Find the area of the region lying in the first quadrant bounded by the region y = 4x2, x = 0, y = 0 and y = 4
Choose the correct alternative:
Area bounded by the curve y = x(4 – x) between the limits 0 and 4 with x-axis is
Choose the correct alternative:
Area bounded by the curve y = e–2x between the limits 0 ≤ x ≤ `oo` is
Choose the correct alternative:
Area bounded by the curve y = `1/x` between the limits 1 and 2 is
Choose the correct alternative:
Area bounded by y = ex between the limits 0 to 1 is
Choose the correct alternative:
The area bounded by the parabola y2 = 4x bounded by its latus rectum is
Choose the correct alternative:
Area bounded by y = |x| between the limits 0 and 2 is
Find the area of the region bounded by the curve between the parabola y = 8x2 – 4x + 6 the y-axis and the ordinate at x = 2
Find the area of the region bounded by the curve y2 = 27x3 and the lines x = 0, y = 1 and y = 2
