Advertisements
Advertisements
प्रश्न
Find the area bounded by the curve y2 = 36x, the line x = 2 in first quadrant
उत्तर
Given equation of the curve is y2 = 36x
∴ y = `+- sqrt(36x)`
∴ y = `6sqrt(x)` .....[∵ In first quadrant, y > 0]
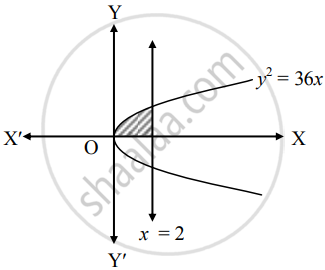
Required area = `int_0^2 y "d"x`
= `int_0^2 6sqrt(x) "d"x`
= `6[(x^(3/2))/(3/2)]_0^2`
= `4[(2)^(3/2) - 0]`
= `4(2sqrt(2))`
= `8sqrt(2)` sq.units
संबंधित प्रश्न
Find the area of the region bounded by the following curves, X-axis and the given lines: x = 2y, y = 0, y = 4
Find the area of the region bounded by the following curves, X-axis and the given lines : x = 0, x = 5, y = 0, y = 4
Find the area of the region bounded by the following curves, X-axis and the given lines: xy = 2, x = 1, x = 4
Find the area of the region bounded by the parabola: y = 4 – x2 and the X-axis.
Find the area of the region included between y = x2 + 3 and the line y = x + 3.
Choose the correct option from the given alternatives :
The area of the region enclosed by the curve y = `(1)/x`, and the lines x = e, x = e2 is given by
Choose the correct option from the given alternatives :
The area bounded by the curve y = x3, the X-axis and the lines x = – 2 and x = 1 is
Choose the correct option from the given alternatives :
The area of the region bounded between the line x = 4 and the parabola y2 = 16x is ______.
The area of the region bounded by y = cos x, Y-axis and the lines x = 0, x = 2π is ______.
Choose the correct option from the given alternatives :
The area bounded by the parabola y2 = 8x, the X-axis and the latus rectum is
Choose the correct option from the given alternatives :
The area under the curve y = `2sqrt(x)`, enclosed between the lines x = 0 and x = 1 is
Choose the correct option from the given alternatives :
The area of the circle x2 + y2 = 25 in first quadrant is
Choose the correct option from the given alternatives :
The area bounded by y = `sqrt(x)` and the x = 2y + 3, X-axis in first quadrant is
Choose the correct option from the given alternatives :
The area bounded by the parabola y = x2 and the line y = x is
Choose the correct option from the given alternatives :
The area enclosed between the two parabolas y2 = 4x and y = x is
The area bounded by the curve y = tan x, X-axis and the line x = `pi/(4)` is ______.
Choose the correct option from the given alternatives :
The area of the region bounded by x2 = 16y, y = 1, y = 4 and x = 0 in the first quadrant, is
Choose the correct option from the given alternatives :
The area of the region included between the line x + y = 1 and the circle x2 + y2 = 1 is
Solve the following :
Find the area of the region bounded by the following curve, the X-axis and the given lines : 0 ≤ x ≤ 5, 0 ≤ y ≤ 2
Solve the following :
Find the area of the region bounded by the following curve, the X-axis and the given lines : y = sin x, x = 0, x = `pi/(3)`
Solve the following :
Find the area of the region bounded by the curve (y – 1)2 = 4(x + 1) and the line y = (x – 1).
Solve the following :
Find the area of the region bounded by the curve y = 4x2, Y-axis and the lines y = 1, y = 4.
The area of the region bounded by the curve y = sinx, X-axis and the lines x = 0, x = 4π is ______ sq.units
The area of the region bounded by the ellipse x2/64 + y2/100 = 1, is ______ sq.units
The area bounded by the curve y2 = x2, and the line x = 8 is ______
The area bounded by the ellipse `x^2/4 + y^2/25` = 1 and the line `x/2 + y/5` = 1 is ______ sq.units
Find the area of the region bounded by the curve y = x2, the X−axis and the given lines x = 0, x = 3
Find the area of the region bounded by the curve y2 = 8x, the X−axis and the given lines x = 1, x = 3, y ≥ 0
Find the area of the region bounded by the curve x2 = 12y, the Y−axis and the given lines y = 2, y = 4, x ≥ 0
Using integration, find the area of the region bounded by the line 2y + x = 8 , X−axis and the lines x = 2 and x = 4
Find the area of the region bounded by the parabola x2 = 4y and The X-axis and the line x = 1, x = 4
Find the area of the region bounded by the parabola y2 = 16x and the line x = 4
Find the area of the region bounded by the curves x2 = 8y, y = 2, y = 4 and the Y-axis, lying in the first quadrant
Find the area of the region bounded by the curve y = sin x, the X−axis and the given lines x = − π, x = π
Find the area of the region bounded by the curves y2 = 4ax and x2 = 4ay
Find the area of the sector bounded by the circle x2+ y2 = 16, and the line y = x in the first quadrant
Find the area of the region bounded by the curve (y − 1)2 = 4(x + 1) and the line y = (x − 1)
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 2 and y = 4.
Find the area of the region bounded by the curve y = x2, and the lines x = 1, x = 2, and y = 0.
