Advertisements
Advertisements
प्रश्न
Find the area of an isosceles triangle whose base is 16 cm and the length of each of the equal sides is 10 cm.
उत्तर
In isosceles Δ ABC
Base BC = 16 cm
and AB = AC = 10 cm

Let AD ⊥ BC and BD = `1/2"BC"=16/2`
∴ BD = 8 cm
In right Δ ABD
AB2 = AD2 + BD2 ..............(Pythagoras Theorem)
(10)2 = AD2 + (8)2
100 = AD2 + 64
100 − 64 = AD2
36 = AD2
AD = `sqrt36=sqrt(6xx6)`
∴ AD = 6 cm
Now, the area of triangle =`("Base"xx"Altitude")/2`
= `(16xx6)/2` = 48 cm2
APPEARS IN
संबंधित प्रश्न
A square lawn is surrounded by a path 2.5 m wide. If the area of the path is 165 m2 find the area of the lawn.
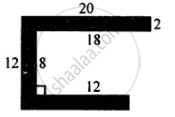
In the figure given below, find the area of shaded region: (All measurements are in cm)
One side of a parallelogram is 20 cm and its distance from the opposite side is 16 cm. Find the area of the parallelogram.
Find the area of a triangle whose base is 30 cm and the height is 18 cm.
The area of a right-angled triangle is 160 cm2. If its one leg is 16 cm long, find the length of the other leg.
Find the area of a right-angled triangle whose hypotenuse is 13 cm long and one of its legs is 12 cm long.
Find the area of an equilateral triangle whose each side is 16 cm. (Take `sqrt3`= 1.73)
The sides of a triangle are 21 cm, 17 cm, and 10 cm. Find its area.
Find the base of a triangle whose area is 360 cm2 and height is 24 cm.
A wire is along the boundary of a circle with a radius of 28 cm. If the same wire is bent in the form of a square, find the area of the square formed.
