Advertisements
Advertisements
Question
Find the area of an isosceles triangle whose base is 16 cm and the length of each of the equal sides is 10 cm.
Solution
In isosceles Δ ABC
Base BC = 16 cm
and AB = AC = 10 cm

Let AD ⊥ BC and BD = `1/2"BC"=16/2`
∴ BD = 8 cm
In right Δ ABD
AB2 = AD2 + BD2 ..............(Pythagoras Theorem)
(10)2 = AD2 + (8)2
100 = AD2 + 64
100 − 64 = AD2
36 = AD2
AD = `sqrt36=sqrt(6xx6)`
∴ AD = 6 cm
Now, the area of triangle =`("Base"xx"Altitude")/2`
= `(16xx6)/2` = 48 cm2
APPEARS IN
RELATED QUESTIONS
A square lawn is surrounded by a path 2.5 m wide. If the area of the path is 165 m2 find the area of the lawn.
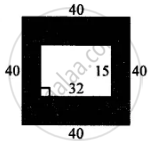
In the figure given below, find the area of shaded region: (All measurements are in cm)
One side of a parallelogram is 20 cm and its distance from the opposite side is 16 cm. Find the area of the parallelogram.
The base of a parallelogram is thrice it height. If its area is 768 cm2, find the base and the height of the parallelogram.
One side of a parallelogram is 18 cm and its area is 153 cm2. Find the distance of the given side from its opposite side.
The sides of a triangle are 21 cm, 17 cm, and 10 cm. Find its area.
Find the base of a triangle whose area is 360 cm2 and height is 24 cm.
The sides of a triangle are in the ratio 15 : 13 : 14 and its perimeter is 168 cm. Find the area of the triangle.
The diameter of the wheel of a car is 70 cm. How many revolutions will it make to travel one kilometer?
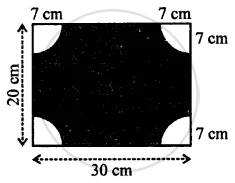
From each corner of a rectangular paper (30 cm x 20 cm) a quadrant of a circle of radius 7 cm is cut. Find the area of the remaining paper i.e., shaded portion.