Advertisements
Advertisements
प्रश्न
Find the area of the ellipse `x^2/a^2 + y^2/b^2 = 1`
उत्तर
Equation of ellipse `x^2/a^2 + y^2/b^2 = 1`
Clearly the area of ellipse is 4 times the area of region OPQO as shown in the figure. For the region, limits of integration are x = 0 and x = a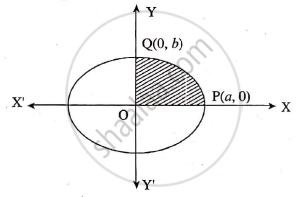
From the equation ellipse,
`x^2/a^2 + y^2/b^2 = 1`
∴ `y^2/b^2 = 1 - x^2/a^2 = ( a^2 - x^2)/a^2`
∴ `y^2 = b^2 ((a^2 - x^2)/a^2)`
∴ `y = +- b/a (a^2 - x^2)^(1/2)`
∴ `y = b/a (a^2 - x^2)^(1/2)`
( ∵ in 1st quadrant y > 0 )
We know,
A = ` 4 int_0^a y dx `
= `4 int_0^a b/a [ (a^2 - x^2) ]^(1/2) dx`
= `(4b)/a [x/2 (a^2 - x^2)^(1/2) + a^2/2 sin^-1(x/a)]_0^a`
= `(4b)/a [{a/a(a^2 - a^2)^(1/2) + a^2/2 sin^(-1)a/a} - {0/a(a^2 - 0^2)^(1/2) + a^2/2 sin^(-1) 0/a}]`
= `(4b)/a [(a^2/2. π/2) - 0]`
= πab sq.units.
