Question

Find the area of the ellipse `x^2/a^2 + y^2/b^2 = 1`

Answer 1

Equation of ellipse `x^2/a^2 + y^2/b^2 = 1`

Clearly the area of ellipse is 4 times the area of region OPQO as shown in the figure. For the region, limits of integration are x = 0 and x = a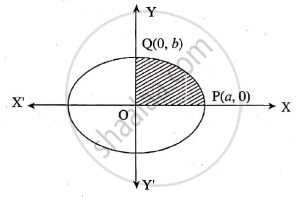

From the equation ellipse,

`x^2/a^2 + y^2/b^2 = 1`
∴ `y^2/b^2 = 1 - x^2/a^2 = ( a^2 - x^2)/a^2`

∴ `y^2 = b^2 ((a^2 - x^2)/a^2)`

∴ `y = +- b/a (a^2 - x^2)^(1/2)`

∴ `y =  b/a (a^2 - x^2)^(1/2)`

                                      ( ∵ in 1st quadrant y > 0 )

We know,

A = ` 4 int_0^a y dx `

    = `4 int_0^a b/a [ (a^2 - x^2) ]^(1/2)  dx`

     = `(4b)/a [x/2 (a^2 - x^2)^(1/2) + a^2/2 sin^-1(x/a)]_0^a` 

= `(4b)/a [{a/a(a^2 - a^2)^(1/2) + a^2/2 sin^(-1)a/a} - {0/a(a^2 - 0^2)^(1/2) + a^2/2 sin^(-1) 0/a}]`

     = `(4b)/a [(a^2/2. π/2) - 0]`

     = πab sq.units.