Advertisements
Advertisements
प्रश्न
Find the asymptotes of the following curves:
f(x) = `(x^2 - 6x - 1)/(x + 3)`
उत्तर
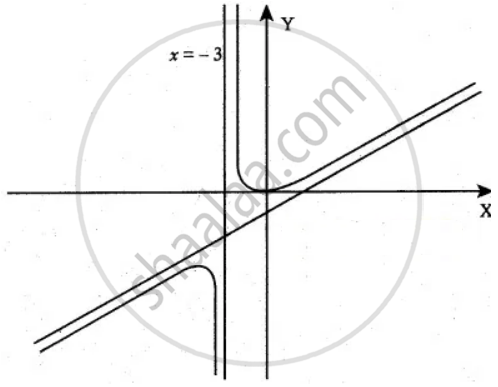
When x = – 3, the function becomes undefined.
∴ x = – 3 is the vertical asymptote.
No Horizontal asymptote exist for the curve.
Oblique asymptote can be obtained by polynomial long division method
`x - 9`
`x + 3")"overline(x^2 - 6x - 1)`
`x^2 + 3x`
(–) (–)
`- 9x - 1`
`- 9x - 27`
(+) (+)
26
∴ y = x – 9 is the slant or oblique asymptote.
APPEARS IN
संबंधित प्रश्न
Find two positive numbers whose sum is 12 and their product is maximum
Find two positive numbers whose product is 20 and their sum is minimum
Find the smallest possible value of x2 + y2 given that x + y = 10
A garden is to be laid out in a rectangular area and protected by a wire fence. What is the largest possible area of the fenced garden with 40 meters of wire?
A rectangular page is to contain 24 cm2 of print. The margins at the top and bottom of the page are 1.5 cm and the margins at the other sides of the page are 1 cm. What should be the dimensions’ of the page so that the area of the paper used is minimum?
A farmer plans to fence a rectangular pasture adjacent to a river. The pasture must contain 1,80,000 sq. mtrs in order to provide enough grass for herds. No fencing is needed along the river. What is the length of the minimum needed fencing material?
Find the dimensions of the rectangle with maximum area that can be inscribed in a circle of radius 10 cm
Prove that among all the rectangles of the given perimeter, the square has the maximum area
A manufacturer wants to design an open box having a square base and a surface area of 108 sq.cm. Determine the dimensions of the box for the maximum volume
The volume of a cylinder is given by the formula V = `pi"r"^2"h"`. Find the greatest and least values of V if r + h = 6
A hollow cone with a base radius of a cm and’ height of b cm is placed on a table. Show that) the volume of the largest cylinder that can be hidden underneath is `4/9` times the volume of the cone
Find the asymptotes of the following curves:
f(x) = `x^2/(x + 1)`
Choose the correct alternative:
One of the closest points on the curve x2 – y2 = 4 to the point (6, 0) is
