Advertisements
Advertisements
प्रश्न
Find the base of an isosceles triangle whose area is 192cm2 and the length of one of the equal sides is 20cm.
उत्तर
Area of an isosceles triangle = 192cm2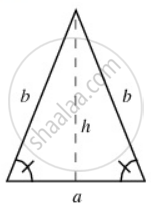
An isosceles triangle is a triangle with (at least) two equal sides. In the figure above, the two equal sides have length b and the remaining side has length a. This property is equivalent to two angles of the triangle being equal. An isosceles triangle therefore has both two equal sides and two equal angles. Let h be the height of the isosceles triangle as illustrated.
So, h = `sqrt("b"^2 - "a"^2/4`
We know that, Area of a Triangle
= `(1)/(2)("Base" xx "Height")`
= `(1)/(2) xx "a" xx "h"`
= `(1)/(2) xx "a" xx sqrt("b"^2 - "a"^2/4)`
= `(1)/(2) xx "a"^2 xx sqrt("b"^2/"a"^2 - 1/4)`
Here, The area is therefore given by
= `(1)/(2) xx x^2 xx sqrt(20^2/x^2 - 1/4)`
= `x^2/(2)sqrt((1600 - x^2)/(4x^2)`
⇒ 192 = `x^2/(2)sqrt((1600 - x^2)/(4x^2)`
⇒ 1922 = `x^4/(4) xx (1600 - x^2)/(4x^2)`
⇒ 1922 x 16 = x2(1600 - x2)
⇒ x4 - 1600x2 + 589824 = 0
⇒ t2 - 1600t + 589824 = 0; wherex2 = t
⇒ t2 - 1024t - 576t + 589824 = 0
⇒ t(t - 1024) - 576(t - 1024) = 0
⇒ t = 1024 or 576
⇒ x2 = 1024 pr 576
⇒ x = 32cm or 24cm.
APPEARS IN
संबंधित प्रश्न
The base of an isosceles triangle is 24 cm and its area is 192 sq. cm. Find its perimeter.
Find the area of an equilateral triangle of side 20 cm.
In a right-angled triangle ABC, if ∠B = 90°, AB - BC = 2 cm; AC - BC = 4 and its perimeter is 24 cm, find the area of the triangle.
A wire when bent in the form of a square encloses an area of 16 cm2. Find the area enclosed by it when the same wire is bent in the form of a rectangle whose sides are in the ratio of 1 : 3
A chessboard contains 64 equal square and the area of each square is 6.25cm2. A 2cm wide border is left inside of the board. Find the length of the side of the chessboard.
Each of the equal sides of an isosceles triangle is 4 cm greater than its height. If the base of the triangle is 24 cm; calculate the perimeter and the area of the triangle.
If in an isosceles triangle, each of the base angles is 40°, then the triangle is ______.
In an isosceles triangle, two angles are always ______.
In an isosceles triangle, angles opposite to equal sides are ______.
Two line segments are congruent, if they are of ______ lengths.
