Question

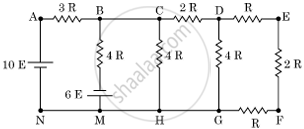
Find the current in branch BM in the network shown:

Answer 1

In the network, resistors R, 2R, and R in the DEFG branch are in series combination.

∴ R' = R + 2R + R = 4 R

and R' and 4R are in parallel combination,

R" = `(4R xx 4R)/(8R)`

= `(16R^2)/(8R)`

= 2R

⇒ R" and 2R are in series combination,

⇒ R''' = R" + 2R = 2R + 2R = 4R

Simplified network of resistors will be

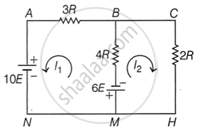
In loop NMBAN,

−6E − 4R(I₁ + I₂) − 3RI₁ − 10E = 0

4RI₂ + 7RI₁ = −16E   ...(i)

In loop BCHMB,

−6E − 4R(I₁ + I₂) − 2RI₂ = 0

4RI₁ +6RI₂ = −6B   ...(ii)

7 × Eq. (ii) − 4 × Eq. (i), we get

(28RI₁ + 42RI₂) − (28RI₁ + 16RI₂) = −42E −(−64E)

⇒ 42RI₂ − 16RI₂ = −42E + 64E

⇒ 26RI₂ = 22E

`I_2 = (22E)/(26R) = 0.84E/R`

Put this value of I₂ in Eq. (i), we get

`4RI_1 = -6E - 6R((22E)/(26R))`

= `-6E(1 + 22/26)`

= `-6E xx 48/26`

= −11.07 E

`I_1 = (-11.07)/4 E/R`

= `-276E/R`        ...(iii)

Hence, current in the branch BM is

`I = I_1 + I_2`

= `-276E/R + 0.84 E/R`

= `-1.92E/R`

Negative sign indicates direction of current is opposite, it flows from M to B in the branch BM.