Advertisements
Advertisements
प्रश्न
Find the locus of a point which is equidistant from (1, 3) and x axis.
उत्तर
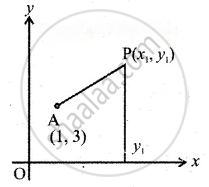
Let P(x1, y1) be any point on the locus.
Let A be the point (1, 3)
The distance from the x-axis on the moving pint P(x1, y1) is y1.
Given that AP = y1
AP2 = `y_1^2`
`(x_1 - 1)^2 + (y_1 - 3)^2 = y_1^2`
`x_1^2 - 2x_1 + 1 + y_1^2 - 6y_1 + 9 = y_1^2`
∴ The locus of the point (x1, y1) is x2 – 2x – 6y + 10 = 0
APPEARS IN
संबंधित प्रश्न
A point moves so that it is always at a distance of 4 units from the point (3, –2)
If the distance of a point from the points (2, 1) and (1, 2) are in the ratio 2 :1, then find the locus of the point.
Find a point on x axis which is equidistant from the points (7, –6) and (3, 4).
If A(-1, 1) and B(2, 3) are two fixed points, then find the locus of a point P so that the area of triangle APB = 8 sq.units.
A point P moves so that P and the points (2, 2) and (1, 5) are always collinear. Find the locus of P.
The locus of the point P which moves such that P is at equidistance from their coordinate axes is:
The locus of a point, which moves such that the sum of squares of its distances from the points (0, 0), (1, 0), (0, 1), (1, 1) is 18 units, is a circle of diameter d. Then d2 is equal to ______.
Let O(0, 0) and A(0, 1) be two fixed points. Then the locus of a point P such that the perimeter of ΔAOP is 4, is ______.
Locus of centroid of the triangle whose vertices are (a cos t, a sin t),(b sin t, – b cos t) and (1, 0), where t is a parameter is ______.
If a variable line drawn through the intersection of the lines `x/3 + y/4` = 1 and `x/4 + y/3` = 1, meets the coordinate axes at A and B, (A ≠ B), then the locus of the midpoint of AB is ______.
