Advertisements
Advertisements
प्रश्न
Find the ratio in which the x-axis divides internally the line joining points A (6, -4) and B ( -3, 8).
उत्तर
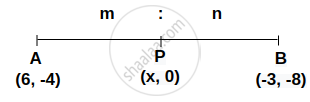
Let 'P'lies on x-axis
∴ Let P = (x, 0)
y = `("my"_2 + "ny"_1)/("m + n")`
`0 = (8"m" - 4"n")/("m + n")`
0 = 8m + 4n
∴ 4n = 8m
`4/8 = "m"/"n"`
`"m"/"n" = 1/2`
Ratio = m : n = 1 : 2
APPEARS IN
संबंधित प्रश्न
Determine the ratio in which the line 3x + y – 9 = 0 divides the segment joining the points (1, 3) and (2, 7)
Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2 : 3.
In what ratio does the point `(24/11, y)` divide the line segment joining the points P(2, –2) and Q(3, 7)? Also find the value of y.
Find the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4).
A line segment joining A`(-1,5/3)` and B(a, 5) is divided in the ratio 1 : 3 at P, the point where the line segment AB intersects the y-axis.
- Calculate the value of ‘a’.
- Calculate the co-ordinates of ‘P’.
If two adjacent vertices of a parallelogram are (3, 2) and (−1, 0) and the diagonals intersect at (2, −5), then find the coordinates of the other two vertices.
The three vertices of a parallelogram ABCD are A(3, −4), B(−1, −3) and C(−6, 2). Find the coordinates of vertex D and find the area of ABCD.
Find the coordinates of a point P, which lies on the line segment joining the points A (−2, −2), and B (2, −4), such that `AP=3/7 AB`.
Find the length of the hypotenuse of a square whose side is 16 cm.
A (30, 20) and B ( 6, -4) are two fixed points. Find the coordinates of a point Pin AB such that 2PB = AP. Also, find the coordinates of some other point Qin AB such that AB = 6 AQ.
