Advertisements
Advertisements
प्रश्न
Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2 : 3.
उत्तर
The end points of AB are A(-1, 7) and B (4, -3)
Therefore `(x_1 = -1, y_1 = 7) and (x_2 = 4, y_2 = -3 )`
Also , m = 2 and n = 3
Let the required point be P (x, y).
By section formula, we get
`x= (("m"x_2 + "n"x_1))/(("m"+"n")) , "y" = (("my"_2+"ny"_1))/(("m"+"n"))`
`⇒ x = ({ 2 xx 4 +3 xx (-1) })/(2+3) , "y"= ({2 xx (-3) + 3 xx 7})/(2+3)`
`⇒ x = (8-3) /5, "y" = (-6+21)/5`
`⇒ x = 5/5, "y" = 15/5`
Therefore, x = 1 and y = 3
Hence, the coordinates of the required point are (1, 3).
APPEARS IN
संबंधित प्रश्न
Find the ratio in which the point P(x, 2) divides the line segment joining the points A(12, 5) and B(4, −3). Also, find the value of x.
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
Find the lengths of the medians of a ∆ABC whose vertices are A(7, –3), B(5,3) and C(3,–1)
If the coordinates of the mid points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4) Find its centroid
Find the coordinates of the points which divide the line segment joining A (−2, 2) and B (2, 8) into four equal parts.
If the mid-point of the line joining (3, 4) and (k, 7) is (x, y) and 2x + 2y + 1 = 0 find the value of k.
If two vertices of a parallelogram are (3, 2) (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
Points A, B, C and D divide the line segment joining the point (5, –10) and the origin in five equal parts. Find the co-ordinates of B and D.
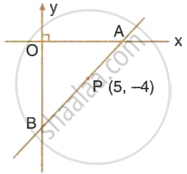
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
The line segment joining the points M(5, 7) and N(–3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
Given a line segment AB joining the points A(−4, 6) and B(8, −3). Find:
- the ratio in which AB is divided by the y-axis.
- find the coordinates of the point of intersection.
- the length of AB.
Find the co-ordinates of the centroid of a triangle ABC whose vertices are: A(–1, 3), B(1, –1) and C(5, 1).
In what ratio does the point (1, a) divided the join of (−1, 4) and (4, −1) Also, find the value of a.
Find the ratio in which the line y = -1 divides the line segment joining (6, 5) and (-2, -11). Find the coordinates of the point of intersection.
Show that the line segment joining the points (-3, 10) and (6, -5) is trisected by the coordinates axis.
Point P(– 4, 6) divides point A(– 6, 10) and B(m, n) in the ratio 2:1, then find the coordinates of point B
If the points A(1, 2), O(0, 0), C(a, b) are collinear, then ______.
The points (-5, 1), (1, p) and (4, -2) are collinear if the value of p is ______.
Find the ratio in which the point `P(3/4, 5/12)` divides the line segment joining the points `A(1/2, 3/2)` and B(2, –5).
Complete the following activity to find the coordinates of point P which divides seg AB in the ratio 3:1 where A(4, – 3) and B(8, 5).
Activity:
∴ By section formula,
∴ x = `("m"x_2 + "n"x_1)/square`,
∴ x = `(3 xx 8 + 1 xx 4)/(3 + 1)`,
= `(square + 4)/4`,
∴ x = `square`,
∴ y = `square/("m" + "n")`
∴ y = `(3 xx 5 + 1 xx (-3))/(3 + 1)`
= `(square - 3)/4`
∴ y = `square`
