Advertisements
Advertisements
प्रश्न
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
उत्तर

Let P (x1, y1) and Q (x2, y2) are the points of trisection of the line segment joining the given points i.e., AP = PQ = QB
Therefore, point P divides AB internally in the ratio 1:2.
∴ `x = (m_1x_2 + m_2x_1)/(m_1 + m_2),` `y = (m_1y_2 + m_2y_1)/(m_1 + m_2)`
`x_1= (1xx(-2)+2xx4)/(1+2), y_1 = (1xx(-3)+2xx(-1))/(1+2)`
`x_1 = (-2+8)/3=6/3=2, y_1 = (-3-2)/3 = (-5)/3`
Therefore, P(x1, y1) = `(2, -5/3)`
Point Q divides AB internally in the ratio 2:1.
∴ `x = (m_1x_2 + m_2x_1)/(m_1 + m_2),` `y = (m_1y_2 + m_2y_1)/(m_1 + m_2)`
`x_2=(2xx(-2)+1xx4)/(2+1), y_2=(2xx(-3)+1xx(-1))/(2+1)`
`x_2 = (-4+4)/3 = 0, y_2= (-6-1)/3 = (-7)/3`
`Q(x_2, y_2) = (0, -7/3)`
APPEARS IN
संबंधित प्रश्न
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) such that AP =(2/5)AB.
Find the ratio in which y-axis divides the line segment joining the points A(5, –6) and B(–1, –4). Also find the coordinates of the point of division.
If the point C (–1, 2) divides internally the line segment joining A (2, 5) and B in ratio 3 : 4, find the coordinates of B
Prove that (4, – 1), (6, 0), (7, 2) and (5, 1) are the vertices of a rhombus. Is it a square?
Find the lengths of the medians of a ∆ABC whose vertices are A(7, –3), B(5,3) and C(3,–1)
If A and B are (−2, −2) and (2, −4), respectively, find the coordinates of P such that `"AP" = 3/7 "AB"` and P lies on the line segment AB.
Find the coordinates of the points which divide the line segment joining A (−2, 2) and B (2, 8) into four equal parts.
In what ratio does the point (a, 6) divide the join of (–4, 3) and (2, 8)? Also, find the value of a.
The line joining the points A (–3, –10) and B (–2, 6) is divided by the point P such that `(PB)/(AB) = 1/5`. Find the co-ordinates of P.
A (2, 5), B (–1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that : AP : PB = AQ : QC = 1 : 2.
- Calculate the co-ordinates of P and Q.
- Show that : `PQ = 1/3 BC`.
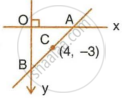
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
The mid point of the line segment joining (4a, 2b – 3) and (−4, 3b) is (2, –2a). Find the values of a and b.
The points A, B and C divides the line segment MN in four equal parts. The coordinates of Mand N are (-1, 10) and (7, -2) respectively. Find the coordinates of A, B and C.
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P (- 3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.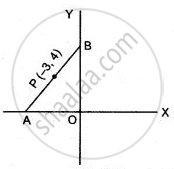
The point Q divides segment joining A(3, 5) and B(7, 9) in the ratio 2 : 3. Find the X-coordinate of Q
Find the ratio in which Y-axis divides the point A(3, 5) and point B(– 6, 7). Find the coordinates of the point
If `P(a/3, 4)` is the mid-point of the line segment joining the points Q(– 6, 5) and R(– 2, 3), then the value of a is ______.
The fourth vertex D of a parallelogram ABCD, whose three vertices are A(–2, 3), B(6, 7) and C(8, 3), is ______.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. What are the coordinates of the centroid of the triangle ABC?
Read the following passage:
Jagdish has a field which is in the shape of a right angled triangle AQC. He wants to leave a space in the form of a square PQRS inside the field for growing wheat and the remaining for growing vegetables (as shown in the figure). In the field, there is a pole marked as O. |
Based on the above information, answer the following questions :
- Taking O as origin, coordinates of P are (–200, 0) and of Q are (200, 0). PQRS being a square, what are the coordinates of R and S?
- (a) What is the area of square PQRS?
OR
(b) What is the length of diagonal PR in square PQRS? - If S divides CA in the ratio K : 1, what is the value of K, where point A is (200, 800)?
