Advertisements
Advertisements
प्रश्न
Read the following passage:
Jagdish has a field which is in the shape of a right angled triangle AQC. He wants to leave a space in the form of a square PQRS inside the field for growing wheat and the remaining for growing vegetables (as shown in the figure). In the field, there is a pole marked as O. |
Based on the above information, answer the following questions :
- Taking O as origin, coordinates of P are (–200, 0) and of Q are (200, 0). PQRS being a square, what are the coordinates of R and S?
- (a) What is the area of square PQRS?
OR
(b) What is the length of diagonal PR in square PQRS? - If S divides CA in the ratio K : 1, what is the value of K, where point A is (200, 800)?
उत्तर
i. Since, PQRS is a square
∴ PQ = QR = RS = PS
Length of PQ = 200 – (–200) = 400
∴ The coordinates of R = (200, 400)
and coordinates of S = (–200, 400)
ii. (a) Area of square PQRS = (side) 2
= (PQ)2
= (400)2
= 1,60,000 sq. units
OR
(b) By Pythagoras theorem
(PR)2 = (PQ)2 + (QR)2
= 1,60,000 + 1,60,000
= 3,20,000
`\implies` PR = `sqrt(3,20,000)`
= `400 xx sqrt(2)` units
iii. Since, point S divides CA in the ratio K : 1
∴ `((Kx_2 + x_1)/(K + 1), (Ky_2 + y_1)/(K + 1))` = (–200, 400)
`implies ((K(200) + (-600))/(K + 1), (K(800) + 0)/(K + 1))` = (–200, 400)
`implies ((200K - 600)/(K + 1), (800K)/(K + 1))` = (–200, 400)
∴ `(800K)/(K + 1)` = 400
`implies` 800K = 400K + 400
`implies` 400K = 400
`implies` K = 1
APPEARS IN
संबंधित प्रश्न
If the coordinates of the mid-points of the sides of a triangle are (1, 2) (0, –1) and (2, 1). Find the coordinates of its vertices.
Show that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10).
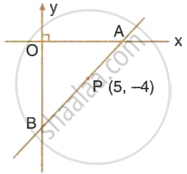
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
Show that the line segment joining the points (–5, 8) and (10, −4) is trisected by the co-ordinate axes.
If A = (−4, 3) and B = (8, −6)
- Find the length of AB.
- In what ratio is the line joining A and B, divided by the x-axis?
The line segment joining A (2, 3) and B (6, –5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K.
The line joining P(–4, 5) and Q(3, 2) intersects the y-axis at point R. PM and QN are perpendicular from P and Q on the x-axis Find:
- the ratio PR : RQ
- the coordinates of R.
- the area of the quadrilateral PMNQ.
A (2, 5), B (-1, 2) and C (5, 8) are the vertices of triangle ABC. Point P and Q lie on AB and AC respectively, such that AP: PB = AQ: QC = 1: 2. Calculate the coordinates of P and Q. Also, show that 3PQ = BC.
Find the coordinates of the point R on the line segment joining the points P(–1, 3) and Q(2, 5) such that PR = `3/5` PQ.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
