Advertisements
Advertisements
प्रश्न
The line joining the points A (–3, –10) and B (–2, 6) is divided by the point P such that `(PB)/(AB) = 1/5`. Find the co-ordinates of P.
उत्तर
Let the co-ordinates of P be (x, y) which divides the line joining the points A (–3, –10) and B (–2, 6) in the ratio of AP : PB i.e. (5 – 1) : 1 or 4 : 1
Since 5 PB = PA + PB
`\implies` 4 PB = PA
`\implies (PA)/(PB) = 4/1`
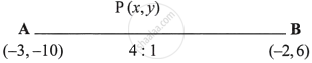
∴ `x = (4 xx (-2) + 1 xx (-3))/(4 + 1)`
= `(-8 - 3)/5`
= `(-11)/5`
`y = (4 xx 6 + 1 xx (-10))/(4 + 1)`
= `(24 - 10)/5`
= `14/5`
∴ Co-ordinates of P are `((-11)/5, 14/5)`
APPEARS IN
संबंधित प्रश्न
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (− 1, 4) and (− 2, −1) taken in order.
[Hint: Area of a rhombus = `1/2` (product of its diagonals)]
If the points (-2, -1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x and y.
Show that A (3, –2) is a point of trisection of the line segment joining the points (2, 1) and (5, −8). Also, find the co-ordinates of the other point of trisection.
If A = (−4, 3) and B = (8, −6)
- Find the length of AB.
- In what ratio is the line joining A and B, divided by the x-axis?
In what ratio is the line joining A(0, 3) and B(4, –1) divided by the x-axis? Write the co-ordinates of the point where AB intersects the x-axis.
Show that the line segment joining the points (-3, 10) and (6, -5) is trisected by the coordinates axis.
If the points A(1, –2), B(2, 3) C(a, 2) and D(– 4, –3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base.
Find the ratio in which the x-axis divides internally the line joining points A (6, -4) and B ( -3, 8).
In what ratio does the Y-axis divide the line segment P(– 3, 1) and Q(6, 2)?
Read the following passage:
Jagdish has a field which is in the shape of a right angled triangle AQC. He wants to leave a space in the form of a square PQRS inside the field for growing wheat and the remaining for growing vegetables (as shown in the figure). In the field, there is a pole marked as O. |
Based on the above information, answer the following questions :
- Taking O as origin, coordinates of P are (–200, 0) and of Q are (200, 0). PQRS being a square, what are the coordinates of R and S?
- (a) What is the area of square PQRS?
OR
(b) What is the length of diagonal PR in square PQRS? - If S divides CA in the ratio K : 1, what is the value of K, where point A is (200, 800)?
