Advertisements
Advertisements
प्रश्न
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured clockwise.
उत्तर
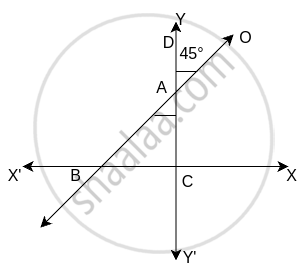
∠DAO = ∠BAC ...[Vertically opposite angels]
∠BAC = 45°
∠ACB = 90°
∠ABC = θ
In △ABC,
∠ABC + ∠ACB + ∠BAC = 180° ...[Property of a △]
θ + 90° + 45° = 180°
θ + 135° = 180°
θ = 180° - 135°
θ = 45°
Slope of the line = tanθ
= tan 45°
= 1
APPEARS IN
संबंधित प्रश्न
Find the slope of the following lines which pass through the point: (2, – 1), (4, 3)
Find the slope of the following lines which pass through the point: (7, 1), (– 3, 1)
Find the slope of the line whose inclination is 30°.
Find the slope of the line whose inclination is 45°.
Find the value of k for which the points P(k, – 1), Q(2, 1) and R(4, 5) are collinear.
Find the slope of the line passing through the following point: (1, 2), (3, – 5)
Find the slope of the line passing through the following point: (1, 3), (5, 2)
Find the slope of the line passing through the following point: (–1, 3), (3, –1)
Find the slope of the line which makes an angle of 120° with the positive X-axis.
Find the slope of the line which makes intercepts 3 and – 4 on the axes.
Find the value of k: the points (1, 3), (4, 1), (3, k) are collinear.
Find the value of k: the point P(1, k) lies on the line passing through the points A(2, 2) and B(3, 3).
Find the slope of the line y – x + 3 = 0.
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Obtain the equation of the line containing the point: (2, 4) and perpendicular to the Y−axis.
Find the equation of the line: containing the point T(7, 3) and having inclination 90°.
