Advertisements
Advertisements
Question
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured clockwise.
Solution
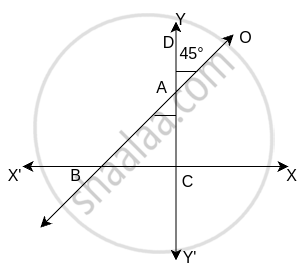
∠DAO = ∠BAC ...[Vertically opposite angels]
∠BAC = 45°
∠ACB = 90°
∠ABC = θ
In △ABC,
∠ABC + ∠ACB + ∠BAC = 180° ...[Property of a △]
θ + 90° + 45° = 180°
θ + 135° = 180°
θ = 180° - 135°
θ = 45°
Slope of the line = tanθ
= tan 45°
= 1
APPEARS IN
RELATED QUESTIONS
Find the slope of the following lines which pass through the point: (2, – 1), (4, 3)
Find the slope of the following lines which pass through the point: (– 2, 3), (5, 7)
Find the slope of the following lines which pass through the point: (2, 3), (2, – 1)
If the X and Y-intercepts of line L are 2 and 3 respectively, then find the slope of line L.
Find the slope of the line whose inclination is 30°.
A line makes intercepts 3 and 3 on coordinate axes. Find the inclination of the line.
Find the slope of the line passing through the following point: (1, 3), (5, 2)
Find the slope of the line passing through the following point: (–1, 3), (3, –1)
Find the slope of the line which makes an angle of 120° with the positive X-axis.
Find the slope of the line which passes through the points A(–2, 1) and the origin.
Find the value of k: if the slope of the line passing through the points (3, 4), (5, k) is 9.
Find the value of k: the points (1, 3), (4, 1), (3, k) are collinear.
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Obtain the equation of the line containing the point: (2, 4) and perpendicular to the Y−axis.
Obtain the equation of the line containing the point: (2, 5) and perpendicular to the X−axis.
