Advertisements
Advertisements
Question
A line makes intercepts 3 and 3 on coordinate axes. Find the inclination of the line.
Solution
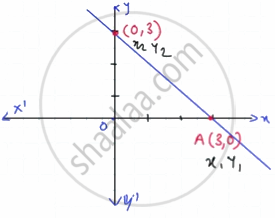
x intercept = 3
y intercept = 3
θ = ?
Slope = `(y_2 - y_1)/(x_2 - x_1) = (3 - 0)/(0 - 3) = 3/(-3) = -1`
m = -1
tanθ = `-tan pi/4`
tan(π - θ) = -tanθ
tanθ = -1
tanθ = tan`(pi - pi/4)`
tanθ = `tan((4pi - pi)/4)`
tanθ = `tan (3pi)/4`
θ = `(3pi)/4`
APPEARS IN
RELATED QUESTIONS
Find the slope of the following lines which pass through the point: (– 2, 3), (5, 7)
Find the slope of the following lines which pass through the point: (2, 3), (2, – 1)
Find the slope of the following lines which pass through the point: (7, 1), (– 3, 1)
Find the slope of the line whose inclination is 45°.
Without using Pythagoras theorem, show that points A (4, 4), B (3, 5) and C (– 1, – 1) are the vertices of a right-angled triangle.
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured clockwise.
Find the slope of the line passing through the following point: (1, 3), (5, 2)
Find the slope of the line passing through the following point: (2, – 5), (3, – 1)
Find the slope of the line which makes an angle of 120° with the positive X-axis.
Find the slope of the line which makes intercepts 3 and – 4 on the axes.
Find the slope of the line which passes through the points A(–2, 1) and the origin.
Find the value of k: if the slope of the line passing through the points (3, 4), (5, k) is 9.
Find the value of k: the point P(1, k) lies on the line passing through the points A(2, 2) and B(3, 3).
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Obtain the equation of the line containing the point: (2, 4) and perpendicular to the Y−axis.
Find the equation of the line: containing the point T(7, 3) and having inclination 90°.
Find the equation of the line: containing the origin and having inclination 90°.
