Advertisements
Advertisements
प्रश्न
Find tn for the A.P. 3,8,13,18,.....
उत्तर
A.P : 3,8,13,18,.....
Here , a = 3
d = t2 -t1
= 8 - 3
d = 5
tn = a + (n - 1)d
tn = 3 + (n - 1)5
= 5n - 2
tn = 5n - 2
APPEARS IN
संबंधित प्रश्न
Find the sum of all three-digits natural numbers which are divisible by 13.
In an AP, the first term is 2, the last term is 29 and the sum of all the terms is 155. Find the common difference.
In an AP, the first term is -4, the last term is 29 and the sum of all its terms is 150. Find its common difference.
In an AP, the first term is 22, nth terms is -11 and sum of first n terms is 66. Find the n and hence find the4 common difference.
The 12th term of an AP is -13 and the sum of its first four terms is 24. Find the sum of its first 10 terms.
The sum of the first 7 terms of an AP is 182. If its 4th and 17th terms are in the ratio 1:5, find the AP.
The sum first 10 terms of an AP is -150 and the sum of its next 10 terms is -550 . Find the AP.
The 16th term of an AP is 5 times its 3rd term. If its 10th term is 41, find the sum of its first 15 terms.
The sum of fist m terms of an AP is ( 4m2 - m). If its nth term is 107, find the value of n. Also, Find the 21st term of this AP.
Is the following sequences are A.P.? If is A.P. find the common difference.
0, –4, –8, –12,...
Which of the following sequences are A.P.? If they are A.P. find the common difference.
`3, 3 + sqrt2, 3 + 2sqrt2, 3 + 3sqrt2, ...`
Write the correct number in the given boxes from the following A. P.
–3, –8, –13, –18,...
Here t3 =  , t2 =
, t2 =  , t4 =
, t4 = , t1 =
, t1 =  ,
,
t2 – t1 =  , t3 – t2 =
, t3 – t2 =  ∴ a =
∴ a =  , d =
, d = 
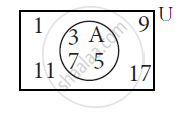
Observe the adjacent Venn diagram and write the complement of A.
Find the class-mark of 80-90.
Yogesh requires 3 days more than Vivek to do a work completely. If both
of them work together, the work can be completed in 2 days. Find the
number of days required for each of them to do the work completely.
In the A.P. 2, –2, –6, –10, ..... common difference (d) is ______.
Find S2 for the A.P. 3,5,7,9,......
Find the value of the determinate:
`|(4,-2),(3,1)|`
