Advertisements
Advertisements
प्रश्न
Find x if distance between points L(x, 7) and M(1, 15) is 10.
उत्तर १
L(x, 7), M(1, 15), and LM = 10.
By distance formula,
∴ LM = `sqrt((x − 1)^2 + (7 − 15)^2)`
∴ 10 = `sqrt((x - 1)^2 + (− 8)^2)`
Squaring both the sides, we get,
∴ 100 = (x − 1)2 + 64
∴ (x − 1)2 = 100 − 64
∴ (x − 1)2 = 36
Taking square roots of both the sides,
∴ x − 1 = `+-` 6
∴ x − 1 = 6 or x - 1 = −6
∴ x = 6 + 1 or x = −6 + 1
∴ x = 7 or x = −5
x = 7 or x = −5
उत्तर २
L(x, 7), M(1, 15), and LM = 10.
By distance formula,
∴ LM = `sqrt((x − 1)^2 + (7 − 15)^2)`
∴ 10 = `sqrt((x - 1)^2 + (− 8)^2)`
Squaring both the sides, we get,
∴ 100 = (x − 1)2 + 64
∴ 100 = x2 − 2x + 1 + 64
∴ 100 = x2 − 2x + 65
∴ x2 − 2x + 65 − 100 = 0
∴ x2 − 2x − 35 = 0
∴ x2 − 7x + 5x - 35 = 0
∴ x(x − 7) + 5(x − 7) = 0
∴ (x − 7)(x + 5) = 0
∴ x − 7 = 0 or x + 5 = 0
∴ x = 7 or x = −5
x = 7 or x = −5
APPEARS IN
संबंधित प्रश्न
If A(4, 3), B(-1, y) and C(3, 4) are the vertices of a right triangle ABC, right-angled at A, then find the value of y.
If the point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), find p. Also, find the length of AB.
If the point (x, y) is equidistant from the points (a + b, b – a) and (a – b, a + b), prove that bx = ay
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(- 1, - 2), (1, 0), (- 1, 2), (- 3, 0)
Name the type of quadrilateral formed, if any, by the following point, and give reasons for your answer:
(−3, 5), (3, 1), (0, 3), (−1, −4)
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (−3, 4).
The length of a line segment is of 10 units and the coordinates of one end-point are (2, -3). If the abscissa of the other end is 10, find the ordinate of the other end.
Prove that the points A(1, 7), B (4, 2), C(−1, −1) D (−4, 4) are the vertices of a square.
An equilateral triangle has two vertices at the points (3, 4) and (−2, 3), find the coordinates of the third vertex.
Find all possible values of x for which the distance between the points
A(x,-1) and B(5,3) is 5 units.
Find the distance between the following pair of point.
P(–5, 7), Q(–1, 3)
Find the distance between the following pairs of point in the coordinate plane :
(13 , 7) and (4 , -5)
Find the coordinate of O , the centre of a circle passing through A (8 , 12) , B (11 , 3), and C (0 , 14). Also , find its radius.
In what ratio does the point P(−4, y) divides the line segment joining the points A(−6, 10) and B(3, −8)? Hence find the value of y.
Find distance between point A(–1, 1) and point B(5, –7):
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = – 7
Using distance formula,
d(A, B) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
∴ d(A, B) = `sqrt(square +[(-7) + square]^2`
∴ d(A, B) = `sqrt(square)`
∴ d(A, B) = `square`
If the distance between point L(x, 7) and point M(1, 15) is 10, then find the value of x
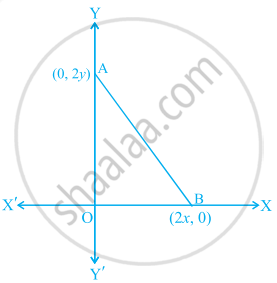
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
If the distance between the points (4, P) and (1, 0) is 5, then the value of p is ______.
The equation of the perpendicular bisector of line segment joining points A(4,5) and B(-2,3) is ______.
Points A(4, 3), B(6, 4), C(5, –6) and D(–3, 5) are the vertices of a parallelogram.
