Advertisements
Advertisements
प्रश्न
Find distance between point A(–1, 1) and point B(5, –7):
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = – 7
Using distance formula,
d(A, B) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
∴ d(A, B) = `sqrt(square +[(-7) + square]^2`
∴ d(A, B) = `sqrt(square)`
∴ d(A, B) = `square`
उत्तर
Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = – 7
Using distance formula,
d(A, B) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
∴ d(A, B) = `sqrt([5 - (-1)]^2 + [(-7) + -1]^2`
∴ d(A, B) = `sqrt(6^2 + (-8)^2`
∴ d(A, B) = `sqrt(36 + 64)`
∴ d(A, B) = `sqrt(100)`
∴ d(A, B) = 10 units
APPEARS IN
संबंधित प्रश्न
If A (-1, 3), B (1, -1) and C (5, 1) are the vertices of a triangle ABC, find the length of the median through A.
Find the co-ordinates of points of trisection of the line segment joining the point (6, –9) and the origin.
Find the distance between the points
(ii) A(7,-4)and B(-5,1)
Determine whether the points are collinear.
A(1, −3), B(2, −5), C(−4, 7)
Determine whether the point is collinear.
R(0, 3), D(2, 1), S(3, –1)
Find the distance of the following point from the origin :
(5 , 12)
Find the point on the x-axis equidistant from the points (5,4) and (-2,3).
Prove that the points (1 ,1),(-4 , 4) and (4 , 6) are the certices of an isosceles triangle.
From the given number line, find d(A, B):

A point A is at a distance of `sqrt(10)` unit from the point (4, 3). Find the co-ordinates of point A, if its ordinate is twice its abscissa.
Point P (2, -7) is the center of a circle with radius 13 unit, PT is perpendicular to chord AB and T = (-2, -4); calculate the length of: AT

KM is a straight line of 13 units If K has the coordinate (2, 5) and M has the coordinates (x, – 7) find the possible value of x.
Find distance between point A(7, 5) and B(2, 5)
The distance of the point P(–6, 8) from the origin is ______.
A circle has its centre at the origin and a point P(5, 0) lies on it. The point Q(6, 8) lies outside the circle.
Find the value of a, if the distance between the points A(–3, –14) and B(a, –5) is 9 units.
If (a, b) is the mid-point of the line segment joining the points A(10, –6) and B(k, 4) and a – 2b = 18, find the value of k and the distance AB.
|
Case Study Trigonometry in the form of triangulation forms the basis of navigation, whether it is by land, sea or air. GPS a radio navigation system helps to locate our position on earth with the help of satellites. |
- Make a labelled figure on the basis of the given information and calculate the distance of the boat from the foot of the observation tower.
- After 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(`sqrt(3)` - 1) m. He immediately raised the alarm. What was the new angle of depression of the boat from the top of the observation tower?
|
In a GPS, The lines that run east-west are known as lines of latitude, and the lines running north-south are known as lines of longitude. The latitude and the longitude of a place are its coordinates and the distance formula is used to find the distance between two places. The distance between two parallel lines is approximately 150 km. A family from Uttar Pradesh planned a round trip from Lucknow (L) to Puri (P) via Bhuj (B) and Nashik (N) as shown in the given figure below.
|
Based on the above information answer the following questions using the coordinate geometry.
- Find the distance between Lucknow (L) to Bhuj (B).
- If Kota (K), internally divide the line segment joining Lucknow (L) to Bhuj (B) into 3 : 2 then find the coordinate of Kota (K).
- Name the type of triangle formed by the places Lucknow (L), Nashik (N) and Puri (P)
[OR]
Find a place (point) on the longitude (y-axis) which is equidistant from the points Lucknow (L) and Puri (P).
Read the following passage:
|
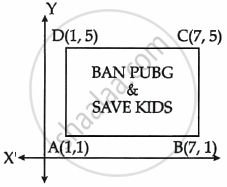
Use of mobile screen for long hours makes your eye sight weak and give you headaches. Children who are addicted to play "PUBG" can get easily stressed out. To raise social awareness about ill effects of playing PUBG, a school decided to start 'BAN PUBG' campaign, in which students are asked to prepare campaign board in the shape of a rectangle: One such campaign board made by class X student of the school is shown in the figure.
|
Based on the above information, answer the following questions:
- Find the coordinates of the point of intersection of diagonals AC and BD.
- Find the length of the diagonal AC.
-
- Find the area of the campaign Board ABCD.
OR - Find the ratio of the length of side AB to the length of the diagonal AC.
- Find the area of the campaign Board ABCD.