SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC chapter 5 - Co-ordinate Geometry [Latest edition]

Point P is midpoint of segment AB where A(– 4, 2) and B(6, 2), then the coordinates of P are ______

The distance between point P(2, 2) and Q(5, x) is 5 cm, then the value of x ______

The distance between points P(–1, 1) and Q(5, –7) is ______

If the length of the segment joining point L(x, 7) and point M(1, 15) is 10 cm, then the value of x is ______

Find distance between point A(– 3, 4) and origin O

If point P(1, 1) divide segment joining point A and point B(–1, –1) in the ratio 5 : 2, then the coordinates of A are ______

If segment AB is parallel Y-axis and coordinates of A are (1, 3), then the coordinates of B are ______

If point P is midpoint of segment joining point A(– 4, 2) and point B(6, 2), then the coordinates of P are ______

If point P divides segment AB in the ratio 1 : 3 where A(– 5, 3) and B(3, – 5), then the coordinates of P are ______

If the sum of X-coordinates of the vertices of a triangle is 12 and the sum of Y-coordinates is 9, then the coordinates of centroid are ______

Find the coordinates of the point of intersection of the graph of the equation x = 2 and y = – 3

Find distance between point A(7, 5) and B(2, 5)

The coordinates of diameter AB of a circle are A(2, 7) and B(4, 5), then find the coordinates of the centre

Write the X-coordinate and Y-coordinate of point P(– 5, 4)

What are the coordinates of origin?

Find distance of point A(6, 8) from origin

Find coordinates of midpoint of segment joining (– 2, 6) and (8, 2)

Find the coordinates of centroid of a triangle whose vertices are (4, 7), (8, 4) and (7, 11)

Find distance between points O(0, 0) and B(– 5, 12)

Find coordinates of midpoint of the segment joining points (0, 2) and (12, 14)

Find distance between point Q(3, – 7) and point R(3, 3)

Solution: Suppose Q(x₁, y₁) and point R(x₂, y₂)

x₁ = 3, y₁ = – 7 and x₂ = 3, y₂ = 3

Using distance formula,

d(Q, R) = `sqrt(square)`

∴ d(Q, R) = `sqrt(square - 100)`

∴ d(Q, R) =  `sqrt(square)`

∴ d(Q, R) = `square`

Find distance between point A(–1, 1) and point B(5, –7):

Solution: Suppose A(x₁, y₁) and B(x₂, y₂)

x₁ = –1, y₁ = 1 and x₂ = 5, y₂ = – 7

Using distance formula,

d(A, B) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`

∴ d(A, B) = `sqrt(square +[(-7) + square]^2`

∴ d(A, B) = `sqrt(square)`

∴ d(A, B) = `square`

Find coordinates of the midpoint of a segment joining point A(–1, 1) and point B(5, –7)

Solution: Suppose A(x₁, y₁) and B(x₂, y₂)

x₁ = –1, y₁ = 1 and x₂ = 5, y₂ = –7

Using midpoint formula,

∴ Coordinates of midpoint of segment AB 

= `((x_1 + x_2)/2, (y_1+ y_2)/2)`

= `(square/2, square/2)`

∴ Coordinates of the midpoint = `(4/2, square/2)`

∴ Coordinates of the midpoint = `(2, square)`

The coordinates of the vertices of a triangle ABC are A (–7, 6), B(2, –2) and C(8, 5). Find coordinates of its centroid.

Solution: Suppose A(x₁, y₁) and B(x₂, y₂) and C(x₃, y₃)

 x₁ = –7, y₁ = 6 and x₂ = 2, y₂ = –2 and x₃ = 8, y₃ = 5

Using Centroid formula

∴ Coordinates of the centroid of a traingle

ABC = `((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`

= `(square/3, square/3)`

∴ Coordinates of the centroid of a triangle ABC = `(3/3, square)`

∴ Coordinates of the centroid of a triangle ABC = `(1 , square)`

The point Q divides segment joining A(3, 5) and B(7, 9) in the ratio 2 : 3. Find the X-coordinate of Q

If the distance between point L(x, 7) and point M(1, 15) is 10, then find the value of x

Find the coordinates of midpoint of segment joining (22, 20) and (0, 16)

Find distance CD where C(– 3a, a), D(a, – 2a)

Show that the point (11, – 2) is equidistant from (4, – 3) and (6, 3)

If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio

Solution:

Point P divides segment AB in the ratio m: n.

A(8, 9) = (x₁, y₁), B(1, 2 ) = (x₂, y₂) and P(6, 7) = (x, y)

Using Section formula of internal division,

∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`

∴ 7m + 7n = `square` + 9n

∴ 7m – `square` = 9n – `square`

∴ `square` = 2n

∴ `"m"/"n" = square`

From the figure given alongside, find the length of the median AD of triangle ABC. Complete the activity.

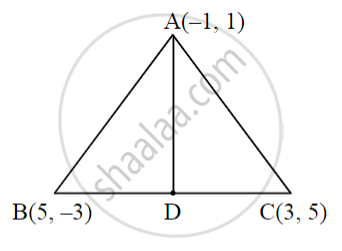
Solution:

Here A(–1, 1), B(5, – 3), C(3, 5) and suppose D(x, y) are coordinates of point D.

Using midpoint formula,

x = `(5 + 3)/2`

∴ x = `square`

y = `(-3 + 5)/2`

∴ y = `square`

Using distance formula,

∴ AD = `sqrt((4 - square)^2 + (1 - 1)^2`

∴ AD = `sqrt((square)^2 + (0)^2`

∴ AD = `sqrt(square)`

∴ The length of median AD = `square`

Show that P(– 2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle

Show that the point (0, 9) is equidistant from the points (– 4, 1) and (4, 1)

Point P(– 4, 6) divides point A(– 6, 10) and B(m, n) in the ratio 2:1, then find the coordinates of point B

Show that points A(– 4, –7), B(–1, 2), C(8, 5) and D(5, – 4) are the vertices of a parallelogram ABCD

Show that the points (0, –1), (8, 3), (6, 7) and (– 2, 3) are vertices of a rectangle.

Show that the points (2, 0), (– 2, 0) and (0, 2) are vertices of a triangle. State the type of triangle with reason

If A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a ∆ABC. Segment AD is median. Find the length of seg AD:

Show that A(1, 2), (1, 6), C(1 + 2 `sqrt(3)`, 4) are vertices of a equilateral triangle

Seg OA is the radius of a circle with centre O. The coordinates of point A is (0, 2) then decide whether the point B(1, 2) is on the circle?

Find the ratio in which Y-axis divides the point A(3, 5) and point B(– 6, 7). Find the coordinates of the point

The points (7, – 6), (2, k) and (h, 18) are the vertices of triangle. If (1, 5) are the coordinates of centroid, find the value of h and k

Using distance formula decide whether the points (4, 3), (5, 1), and (1, 9) are collinear or not.