Advertisements
Advertisements
प्रश्न
If A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a ∆ABC. Segment AD is median. Find the length of seg AD:
उत्तर
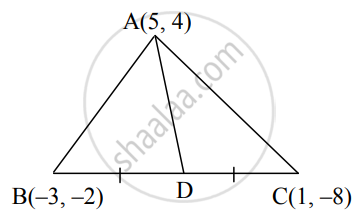
Since segment AD is median, Point D is the midpoint of side BC.
By midpoint formula,
Co-ordinates of D = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
= `((-3 + 1)/2, (-2 - 8)/2)`
= `((-2)/2, (-10)/2)`
Co-ordinates of D = (–1, – 5)
Distance between two points = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
By distance formula,
d(A, D) = `sqrt([5 - (-1)]^2 + [4 - (-5)]^2`
= `sqrt((5 + 1)^2 + (4 + 5)^2`
= `sqrt(6^2 + 9^2)`
= `sqrt(36 + 81)`
= `sqrt(117)`
∴ The length of segment AD is `sqrt(117)` units.
APPEARS IN
संबंधित प्रश्न
A(5, 3), B(–1, 1) and C(7, –3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show that : `LM = 1/2 BC`.
(–5, 2), (3, −6) and (7, 4) are the vertices of a triangle. Find the length of its median through the vertex (3, −6).
P(4, 2) and Q(–1, 5) are the vertices of parallelogram PQRS and (–3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.
Find the coordinates of point P if P divides the line segment joining the points A(–1, 7) and B(4, –3) in the ratio 2 : 3.
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–2, –5), Q(4, 3), a : b = 3 : 4
Write the co-ordinates of the point of intersection of graphs of
equations x = 2 and y = -3.
Find the midpoint of the line segment joining the following pair of point :
(4,7) and (10,15)
A triangle is formed by line segments joining the points (5, 1 ), (3, 4) and (1, 1). Find the coordinates of the centroid.
The midpoints of three sides of a triangle are (1, 2), (2, -3) and (3, 4). Find the centroid of the triangle.
AB is a diameter of a circle with centre 0. If the ooordinates of A and 0 are ( 1, 4) and (3, 6 ). Find the ooordinates of B and the length of the diameter.
A(3, 1), B(y, 4) and C(1, x) are vertices of a triangle ABC. P, Q and R are mid - points of sides BC, CA and AB respectively. Show that the centroid of ΔPQR is the same as the centroid ΔABC.
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
The points A(−5, 4), B(−1, −2) and C(5, 2) are the vertices of an isosceles right-angled triangle where the right angle is at B. Find the coordinates of D so that ABCD is a square
The points A(−3, 6), B(0, 7) and C(1, 9) are the mid-points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallelogram.
The coordinates of the point C dividing the line segment joining the points P(2, 4) and Q(5, 7) internally in the ratio 2 : 1 is
The ratio in which the x-axis divides the line segment joining the points A (a1, b1) and B (a2, b2) is
In what ratio does the y-axis divides the line joining the points (−5, 1) and (2, 3) internally
Find the coordinates of the mid-point of the line segment with points A(– 2, 4) and B(–6, –6) on both ends.
Find the coordinates of point P where P is the midpoint of a line segment AB with A(–4, 2) and B(6, 2).
Solution :

Suppose, (–4, 2) = (x1, y1) and (6, 2) = (x2, y2) and co-ordinates of P are (x, y).
∴ According to the midpoint theorem,
x = `(x_1 + x_2)/2 = (square + 6)/2 = square/2 = square`
y = `(y_1 + y_2)/2 = (2 + square)/2 = 4/2 = square`
∴ Co-ordinates of midpoint P are `square`.
