Advertisements
Advertisements
प्रश्न
The ratio in which the x-axis divides the line segment joining the points A (a1, b1) and B (a2, b2) is
पर्याय
b1 : b2
−b1 : b2
a1 : a2
−a1 : a2
उत्तर
−b1 : b2
Explanation;
Hint:
A line divides internally in the ratio m : n the point P is, `(("m"x_2 + "n"x_1)/("m" + "n"), ("m"_2 +"n"y_1)/("m" + "n"))`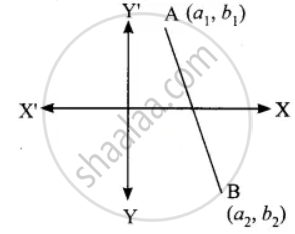
The point P is (a, 0) = `(("ma"_2 + "na"_1)/("m" + "n"), ("mb"_2 + "nb"_1)/("m" "n"))`
∴ `("mb"_2 + "nb"_1)/("m" + "n")` = 0
mb2 + nb1 = 0
⇒ mb2 = −nb1
`"m"/"n" = "b"_1/"b"_2`
∴ m : n = −b1 : b2
APPEARS IN
संबंधित प्रश्न
Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
A(–1, 0), B(1, 3) and D(3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.
The mid-point of the line segment joining A (- 2 , 0) and B (x , y) is P (6 , 3). Find the coordinates of B.
The midpoints of three sides of a triangle are (1, 2), (2, -3) and (3, 4). Find the centroid of the triangle.
A , B and C are collinear points such that AB = `1/2` AC . If the coordinates of A, B and C are (-4 , -4) , (-2 , b) anf (a , 2),Find the values of a and b.
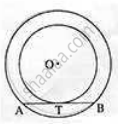
As shown in the figure. two concentric circles are given and line AB is the tangent to the smaller circle at T. Shown that T is the midpoint of Seg AB
Point M is the mid-point of segment AB. If AB = 8.6 cm, then find AM.
Find the mid-point of the line segment joining the points
(−2, 3) and (−6, −5)
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the coordinates of D.
