Advertisements
Advertisements
प्रश्न
If the coordinates of one end of a diameter of a circle is (3, 4) and the coordinates of its centre is (−3, 2), then the coordinate of the other end of the diameter is
पर्याय
(0, −3)
(0, 9)
(3, 0)
(−9, 0)
उत्तर
(−9, 0)
Explanation;
Hint:
Let the other end of the diameter be (a, b)
Mid-point of a line =
`((x_1 + x_2)/2, (y_1 + y_2)/2)`
(−3, 2) = `(3 + "a")/2, (4 + "b")/2`
`(3 + "a")/2` = −3
3 + a = −6
a = −6 – 3 = −9
and
`(4 + "b")/2` = 2
4 + b = 4
b = 4 – 4 = 0
The other end is (−9, 0)
APPEARS IN
संबंधित प्रश्न
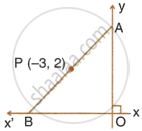
P(–3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.
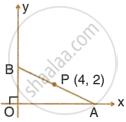
In the given figure, P(4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
Find th co-ordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Find the midpoint of the line segment joining the following pair of point :
(3a-2b, Sa+7b) and (a+4b, a-3b)
Find the mid-point of the line segment joining the points
(a, b) and (a + 2b, 2a – b)
Point P is midpoint of segment AB where A(– 4, 2) and B(6, 2), then the coordinates of P are ______
Find coordinates of midpoint of segment joining (– 2, 6) and (8, 2)
Find the coordinates of midpoint of segment joining (22, 20) and (0, 16)
Find the coordinates of the mid-point of the line segment with points A(– 2, 4) and B(–6, –6) on both ends.
Point P is the centre of the circle and AB is a diameter. Find the coordinates of points B if coordinates of point A and P are (2, – 3) and (– 2, 0) respectively.
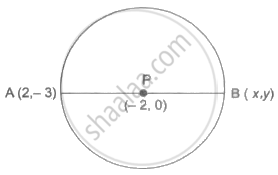
Given: A`square` and P`square`. Let B (x, y)
The centre of the circle is the midpoint of the diameter.
∴ Mid point formula,
`square = (square + x)/square`
⇒ `square = square` + x
⇒ x = `square - square`
⇒ x = – 6
and `square = (square + y)/2`
⇒ `square` + y = 0
⇒ y = 3
Hence coordinates of B is (– 6, 3).
