Advertisements
Advertisements
प्रश्न
A circle has its centre at the origin and a point P(5, 0) lies on it. The point Q(6, 8) lies outside the circle.
पर्याय
True
False
Advertisements
उत्तर
This statement is True.
Explanation:
First, we draw a circle and a point from the given information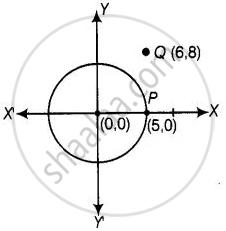
Now, distance between origin i.e., O(0, 0) and P(5, 0),
OP = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
OP = `sqrt((5 - 0)^2 + (0 - 0)^2`
= `sqrt(5^2 + 0^2)`
= 5
= Radius of circle and distance between origin O(0, 0) and Q(6, 8),
OQ = `sqrt((6 - 0)^2 + (8 - 0)^2`
= `sqrt(6^2 + 8^2)`
= `sqrt(36 + 64)`
= `sqrt(100)`
= 10
We know that, if the distance of any point from the centre is less than/equal to/more than the radius, then the point is inside/on/outside the circle, respectively.
Here, we see that, OQ > OP
Hence, it is true that point Q(6, 8), lies outside the circle.
APPEARS IN
संबंधित प्रश्न
Show that four points (0, – 1), (6, 7), (–2, 3) and (8, 3) are the vertices of a rectangle. Also, find its area
If two vertices of an equilateral triangle be (0, 0), (3, √3 ), find the third vertex
If a≠b≠0, prove that the points (a, a2), (b, b2) (0, 0) will not be collinear.
The long and short hands of a clock are 6 cm and 4 cm long respectively. Find the sum of the distances travelled by their tips in 24 hours. (Use π = 3.14) ?
Distance of point (−3, 4) from the origin is ______.
Find the distance of a point (7 , 5) from another point on the x - axis whose abscissa is -5.
Find the point on the x-axis equidistant from the points (5,4) and (-2,3).
Prove that the points (5 , 3) , (1 , 2), (2 , -2) and (6 ,-1) are the vertices of a square.
In what ratio does the point P(−4, y) divides the line segment joining the points A(−6, 10) and B(3, −8)? Hence find the value of y.
The length of line PQ is 10 units and the co-ordinates of P are (2, -3); calculate the co-ordinates of point Q, if its abscissa is 10.
Give the relation that must exist between x and y so that (x, y) is equidistant from (6, -1) and (2, 3).
Show that each of the triangles whose vertices are given below are isosceles :
(i) (8, 2), (5,-3) and (0,0)
(ii) (0,6), (-5, 3) and (3,1).
If the point (x, y) is at equidistant from the point (a + b, b – a) and (a-b, a + b). Prove that ay = bx.
The distance between points P(–1, 1) and Q(5, –7) is ______.
If the distance between the points (4, P) and (1, 0) is 5, then the value of p is ______.
The equation of the perpendicular bisector of line segment joining points A(4,5) and B(-2,3) is ______.
Case Study -2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.
It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.
Each team plays with 11 players on the field during the game including the goalie. Positions you might play include -
- Forward: As shown by players A, B, C and D.
- Midfielders: As shown by players E, F and G.
- Fullbacks: As shown by players H, I and J.
- Goalie: As shown by player K.
Using the picture of a hockey field below, answer the questions that follow:
If a player P needs to be at equal distances from A and G, such that A, P and G are in straight line, then position of P will be given by ______.
If (– 4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
What is the distance of the point (– 5, 4) from the origin?
|
Tharunya was thrilled to know that the football tournament is fixed with a monthly timeframe from 20th July to 20th August 2023 and for the first time in the FIFA Women’s World Cup’s history, two nations host in 10 venues. Her father felt that the game can be better understood if the position of players is represented as points on a coordinate plane. |
- At an instance, the midfielders and forward formed a parallelogram. Find the position of the central midfielder (D) if the position of other players who formed the parallelogram are :- A(1, 2), B(4, 3) and C(6, 6)
- Check if the Goal keeper G(–3, 5), Sweeper H(3, 1) and Wing-back K(0, 3) fall on a same straight line.
[or]
Check if the Full-back J(5, –3) and centre-back I(–4, 6) are equidistant from forward C(0, 1) and if C is the mid-point of IJ. - If Defensive midfielder A(1, 4), Attacking midfielder B(2, –3) and Striker E(a, b) lie on the same straight line and B is equidistant from A and E, find the position of E.
