Advertisements
Advertisements
Question
A circle has its centre at the origin and a point P(5, 0) lies on it. The point Q(6, 8) lies outside the circle.
Options
True
False
Advertisements
Solution
This statement is True.
Explanation:
First, we draw a circle and a point from the given information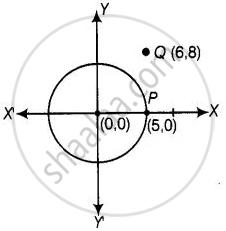
Now, distance between origin i.e., O(0, 0) and P(5, 0),
OP = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
OP = `sqrt((5 - 0)^2 + (0 - 0)^2`
= `sqrt(5^2 + 0^2)`
= 5
= Radius of circle and distance between origin O(0, 0) and Q(6, 8),
OQ = `sqrt((6 - 0)^2 + (8 - 0)^2`
= `sqrt(6^2 + 8^2)`
= `sqrt(36 + 64)`
= `sqrt(100)`
= 10
We know that, if the distance of any point from the centre is less than/equal to/more than the radius, then the point is inside/on/outside the circle, respectively.
Here, we see that, OQ > OP
Hence, it is true that point Q(6, 8), lies outside the circle.
APPEARS IN
RELATED QUESTIONS
If two vertices of an equilateral triangle be (0, 0), (3, √3 ), find the third vertex
Find the coordinates of the centre of the circle passing through the points (0, 0), (–2, 1) and (–3, 2). Also, find its radius.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in the following figure. Champa and Chameli walk into the class and after observing for a few minutes, Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees.
Using distance formula, find which of them is correct.
Find the distance between the points
(ii) A(7,-4)and B(-5,1)
If the point A(x,2) is equidistant form the points B(8,-2) and C(2,-2) , find the value of x. Also, find the value of x . Also, find the length of AB.
Find the distance between the following pair of point.
P(–5, 7), Q(–1, 3)
Find the distance between the following pairs of point in the coordinate plane :
(4 , 1) and (-4 , 5)
Find the distance of a point (13 , -9) from another point on the line y = 0 whose abscissa is 1.
Find the distance between P and Q if P lies on the y - axis and has an ordinate 5 while Q lies on the x - axis and has an abscissa 12 .
Prove that the points (0 , 2) , (1 , 1) , (4 , 4) and (3 , 5) are the vertices of a rectangle.
Find the distance between the following pair of points:
`(sqrt(3)+1,1)` and `(0, sqrt(3))`
Find the point on y-axis whose distances from the points A (6, 7) and B (4, -3) are in the ratio 1: 2.
The distance between point P(2, 2) and Q(5, x) is 5 cm, then the value of x ______
Find distance between points O(0, 0) and B(– 5, 12)
Show that P(– 2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle
Show that A(1, 2), (1, 6), C(1 + 2 `sqrt(3)`, 4) are vertices of a equilateral triangle
Case Study -2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.
It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.
Each team plays with 11 players on the field during the game including the goalie. Positions you might play include -
- Forward: As shown by players A, B, C and D.
- Midfielders: As shown by players E, F and G.
- Fullbacks: As shown by players H, I and J.
- Goalie: As shown by player K.
Using the picture of a hockey field below, answer the questions that follow:
The coordinates of the centroid of ΔEHJ are ______.
The distance between the points A(0, 6) and B(0, –2) is ______.
Find the points on the x-axis which are at a distance of `2sqrt(5)` from the point (7, – 4). How many such points are there?
The point P(–2, 4) lies on a circle of radius 6 and centre C(3, 5).
