Advertisements
Advertisements
Question
The centre of a circle passing through P(8, 5) is (x+l , x-4). Find the coordinates of the centre if the diameter of the circle is 20 units.
Solution
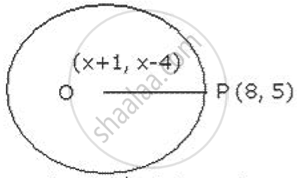
Given diameter of the circle = 20 units.
∴ radius= 10units
OP=10
`sqrt (("x" + 1 - 8)^2 + ("x" - 4 -5)^2) = 10`
squaring both sides,
x2 + 49- 14x + x2 = 81- 18x = 100
⇒ 2x2 - 32x + 30=0
⇒ x2 - 16x + 15=0
⇒ x2 -15x - x +15 = 0
⇒ (x - 15) (x - 1) = 0
⇒ x = 15 or 1
Coordinates of 0when x=15 are (16, 11)
Coordinates of 0 when x = 1 are ( 2, - 3)
APPEARS IN
RELATED QUESTIONS
Given a line segment AB joining the points A(–4, 6) and B(8, –3). Find
1) The ratio in which AB is divided by y-axis.
2) Find the coordinates of the point of intersection.
3) The length of AB.
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two
vertices.
Determine whether the point is collinear.
R(0, 3), D(2, 1), S(3, –1)
AB and AC are the two chords of a circle whose radius is r. If p and q are
the distance of chord AB and CD, from the centre respectively and if
AB = 2AC then proove that 4q2 = p2 + 3r2.
Distance of point (-3, 4) from the origin is .....
(A) 7 (B) 1 (C) 5 (D) 4
Find the distance of a point (13 , -9) from another point on the line y = 0 whose abscissa is 1.
P and Q are two points lying on the x - axis and the y-axis respectively . Find the coordinates of P and Q if the difference between the abscissa of P and the ordinates of Q is 1 and PQ is 5 units.
Find distance between points O(0, 0) and B(– 5, 12)
A circle drawn with origin as the centre passes through `(13/2, 0)`. The point which does not lie in the interior of the circle is ______.
Find the distance between the points O(0, 0) and P(3, 4).
