Advertisements
Advertisements
Question
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two
vertices.
Solution
The distance d between two points `(x_1,y_1)` and `(x_2,y_2)`
`d = sqrt((x_1- x_2)^2 + (y_1 - y_2)^2)`
In a square, all the sides are of equal length. The diagonals are also equal to each other. Also in a square, the diagonal is equal to `sqrt2` times the side of the square.
Here let the two points which are said to be the opposite vertices of a diagonal of a square be A(−1,2) and C(3,2).
Let us find the distance between them which is the length of the diagonal of the square.
`AC = sqrt((-1-3)^2 + (2 - 2)^2 )`
`= sqrt((-4)^2 +(0)^2)`
`= sqrt(16)`
AC = 4
Now we know that in a square,
The side of the square = `"Diagonal of the square"/sqrt2`
The side of the square = `2sqrt2`
Now, a vertex of a square has to be at equal distances from each of its adjacent vertices.
Let P(x, y) represent another vertex of the same square adjacent to both ‘A’ and ‘C’
`AP = sqrt((-1-x)^2 + (2 -y)^2)`
`CP = sqrt((3 - x)^2 + (2 - x)^2)`
But these two are nothing but the sides of the square and need to be equal to each other.
AP = CP
`sqrt((-1-x)^2 + (2 - y)^2) = sqrt((3 - x)^2 + (2 - y)^2)`
Squaring on both sides we have,
`AP = sqrt((-1-x)^2 + (2 - y)^2)`
`2sqrt(2) = sqrt((-1-1)^2 + (2 - y)^2)`
`2sqrt2 = sqrt((-2)^2 + (2 - y)^2)`
Squaring on both sides,
`8 = (-2)^2 + (2 - y)^2`
`8 = 4 + 4 = y^2 - 4y`
`0 = y^2 - 4y`
We have a quadratic equation. Solving for the roots of the equation we have,
`y^2 - 4y = 0`
y(y - 4) = 0
The roots of this equation are 0 and 4.
Therefore the other two vertices of the square are (1, 0) and (1,4)
APPEARS IN
RELATED QUESTIONS
Find the distance between the points
(i) A(9,3) and B(15,11)
Find value of x for which the distance between the points P(x,4) and Q(9,10) is 10 units.
Show that the ▢PQRS formed by P(2, 1), Q(–1, 3), R(–5, –3) and S(–2, –5) is a rectangle.
Find the distance between the following pairs of point in the coordinate plane :
(4 , 1) and (-4 , 5)
Find the distance between the following point :
(Sin θ - cosec θ , cos θ - cot θ) and (cos θ - cosec θ , -sin θ - cot θ)
Prove that the points (1 , 1) , (-1 , -1) and (`- sqrt 3 , sqrt 3`) are the vertices of an equilateral triangle.
PQR is an isosceles triangle . If two of its vertices are P (2 , 0) and Q (2 , 5) , find the coordinates of R if the length of each of the two equal sides is 3.
Show that P(– 2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle
Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter’s school and then reaches the office. What is the extra distance travelled by Ayush in reaching his office? (Assume that all distances covered are in straight lines). If the house is situated at (2, 4), bank at (5, 8), school at (13, 14) and office at (13, 26) and coordinates are in km.
Read the following passage:
|
Alia and Shagun are friends living on the same street in Patel Nagar. Shagun's house is at the intersection of one street with another street on which there is a library. They both study in the same school and that is not far from Shagun's house. Suppose the school is situated at the point O, i.e., the origin, Alia's house is at A. Shagun's house is at B and library is at C. |
Based on the above information, answer the following questions.
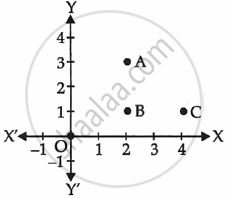
- How far is Alia's house from Shagun's house?
- How far is the library from Shagun's house?
- Show that for Shagun, school is farther compared to Alia's house and library.
OR
Show that Alia’s house, shagun’s house and library for an isosceles right triangle.
